the art of software security assessment Chap6. translate

Posted on | In |
Words count in article: 39.6k | Reading time ≈ 149

7.2 第六章 关于C语言方面的问题(C Language Issues)

“终有一天你将会明白”

—— Neel Mehta ，X-Force互联网安全系统高级研究员

7.2.1 概论

当你正在检查软件并覆盖潜在的安全漏洞时，理解编程语言底层如何实现数据类型以及运算的细节，以及这些细节会如何影响到执行流(execution flow)非常重要。审计员在汇编层面上检查应用程序二进制能够明确地看出数据是怎样存储以及更改的，以及对数据块操作的确切含义。然而，当你在源代码的层面上对应用程序进行审计时，一些细节就显得抽象并且不那么显然了。这种抽象能够导致一些软件中存在微妙的漏洞，这些漏洞在很长时间内不会被注意并修正。一个彻底的审计者应该熟悉源代码使用的语言的底层实现，并且熟悉这些实现细节会如何在边缘情况或者特殊情况下导致安全方面的问题。

本章将会对C语言细微的细节进行探讨，这些细节能够对应用程序的安全以及鲁棒性产生不利的影响。特别地，本章将会讨论原始数据类型(primitive types)的存储，算术溢出以及下溢的情况，类型转换问题，符号位扩展以及截断。你也会看到一些C语言有趣的细微差别， 包括来自某些操作符和其他通常不被重视的行为导致的意外结果。虽然本章的重点是C语言，但很多原则也可以应用到其他语言上。

7.2.2 C语言背景

本章会明确地讨论C语言的特性并且使用从C语言标准中定义的各种术语。你不必去查阅相关标准文献来配合食用，不过本章会明确地使用最新发布的C99标准草案(ISO/IEC 9899:1999)，关于C99标准，可以在下面链接找到： www.open-std.org/jtc1/sc22/wg14/www/standards.

标准草案附带的C Rationale文档也很有用， 有兴趣的读者可以看看Peter Van der Linden的优秀图书Expert C Programming， Kernighan与Ritchie写的The C Programming Language。如果你对购买ISO标准的最终版本或旧的ANSI标准感兴趣的话，两者都在ANSI组织的网站出售 (www.ansi.org).

虽然这一章包含了一个最近的标准，但是内容针对的是目前C的主流使用，特别是ANSI C89/ISO 90标准。因为我们要讨论底层的安全细节，所以会添加关于跨版本C变更相关的任何情况的注释。

在讨论标准时，偶尔会用到术语“未定义的行为”(undefined behavior)和“实现定义的行为”(implementation-defined behavior)。未定义行为是错误行为:编译器不需要处理的条件，因此会产生未指定的结果。实现定义的行为是由底层实现决定的行为。应该以一种一致的、合乎逻辑的方式来处理它，处理它的方法应该文档化。

7.2.3 数据存储概述

在深入研究C的细节之前，应该回顾一下C类型的基础知识，特别是它们的存储大小、值范围和表示。本节从一般的角度解释类型，探索诸如二进制编码、二进制补码算法和字节顺序约定等细节，并以一些常见和未来实现的实用观察作为结束。

C标准将对象定义为执行环境中的数据存储区域;它的内容可以表示值。每个对象都有一个相关联的类型:一种解释存储在该对象中的值并赋予其意义的方法。在C标准中定义了许多类型，但本章主要关注以下内容 ：

  • 字符类型。有三种字符类型，分别是char, signed char, unsigned char。所有三种类型都在存储中占用1个字节，不管char类型是否是带有符号的。大多数系统当前都默认char是带富豪的，尽管编译器的标志(flags)通常能够更改这个行为
  • 整数类型。有4中标准的带符号整数类型，包括short int, int ,long int, long long int。每个标准带符号整数类型都对应了不带符号的整数类型，并且对应的存储大小都相同。(注：long long int是在C99标准时才出现的新类型)
  • 浮点型。有三种实数浮点型和三种复数浮点型。实数浮点型是float, double, long double，三种复数型是float_Complex, double_Complex, long double_Complex。(注：复数类型是C99标准时才出现的新类型。)
  • 位字段(bit fields)。位字段是对象中的特定位数。 位字段可以是带符号的和无符号的，取决于它们的声明。 如果没有给出符号类型说明符，则位字段的符号依赖于实现。

注

位字段可能对于一些程序员来说并不熟悉，因为它们通常不会出现在网络代码(network code)或低层级代码之外。 下面是一个关于位字段的例子：

1
2
3
4
5
6
7
8
9
struct controller
{
    unsigned int id:4;
    unsigned int tflag:1;
    unsigned int rflag:1;
    unsigned int ack:2;
    unsigned int seqnum:8;
    unsigned int code:16;
};

controller结构中有很多数。id表示一个4位的无符号整数，tflag，rflag表示1位，ack是两位，seqnum是8位，code是16位。 这种结构的成员很可能被布局成内存中一个32位区域内的连续位。

从抽象的角度来看，每个整数类型(包括字符类型)都表示了一个占不同大小空间的整数，编译器可以将它们映射到合适的由底层架构决定(underlying architecture-dependent)的数据类型。每个字符会占用1字节的存储(尽管1字节可能不一定等于8位).sizeof(char)会一直是1，你也可以一直使用无符号字符的指针，sizeof和memcpy()来检查和操作其他类型的实际内容。 其他整数类型具有一定范围的值，它们必须能够表示这些值，并且它们之间必须保持一定的关系（例如long不能比short小）， 但除此之外，它们的实现很大程度上取决于它们的架构和编译器。

带符号整数类型能够表示正数和负数，但无符号类型只能表示正数。每个带符号整数类型都有一个对应的无符号整数类型，并且占用相同的存储空间。无符号整数类型有两种不同的位：数位(value bits)包含对象值实际的2进制表示，填充位(padding bits) 是可选的，且标准未指定。带符号整数除了数位和填充位还有额外的一个位：符号位。 如果符号位在有符号整数类型中是清晰的，则其对值的表示与该值在相应的无符号整数类型中的表示相同。 换句话说，不管它是存储在整型还是无符号整型中，正42的底层位模式都应该是相同的。

整数类型有精度和宽度。精度是整型使用的值位数。宽度是类型用于表示其值的位数，包括值和符号位，但不包括填充位。对于无符号整数类型，精度和宽度是相同的。对于有符号整数类型，宽度比精度大1。

程序员能够用多种方式调用不同的类型。对于整数类型，例如short int，程序员通常可以省略int关键字，因此关键字signed short int, signed short, short int和short表示同一数据类型。一般地，如果signed和unsigned关键字被省略了，那么数据类型就会被假定为带符号类型。但是，这种假设对于char类型不成立，因为它是否为带符号取决于具体实现。(通常，char类型是带符号的，如果你想100%确定一个带符号的字符类型，你可以在声明时直接使用signd char。)

C语言还通过typedef 支持丰富的类型别名系统。 因此，程序员通常在指定已知大小和表示形式的变量时做一些约定。例如在UNIX和网络编程中，int8_t, uint8_t, int32_t, u_int32_t就很受程序员欢迎。它们分别表示8位带符号整数，8位无符号整数，32位带符号整数，32位无符号整数。 Windows程序员倾向于使用BYTE、CHAR和DWORD等类型，它们分别对应为8位无符号整数、8位带符号整数和32位无符号整数 。

二进制编码

（这里作者想要cover到所有架构的东西，以至于很多地方为了叙述严谨而导致很啰嗦，建议这一部分参考主要讲述Intel架构的CSAPP —by译者）

无符号整数值通过纯粹的二进制形式进行编码，也就是二进制的计数系统。每个位是0或者1，表示这一位所对应的2的指数所贡献的值。将一个表示为二进制的正数转换为十进制，只需要将第n位对应的数乘以2n−1再全部加起来就可以了，例如下面的例子：

\[00011011=24+23+21+20=27\]

\[00001111=23+22+21+20=15\]

\[00101010=25+23+21=42\]

相近地，将一个十进制表示的正数转换为二进制，只需要不断将它除以2直到结果为0，然后取结果的余数从最高位开始作为对应的数就可以了，例如下面的例子： $$ 55=32+16+4+2+1\

=25+24+22+21+20\

=00110111\

37=32+4+1\

=25+22+20\

=00100101 $$

有符号整数使用符号位以及数位和填充位。C标准给出了三种可能的算术方案，因此也给出了符号位的三种可能解释：

  • 符号和幅度(sign and magnitude)数的符号在符号位中存储，1代表负数0代表正数。数的幅度保存在数位中。这种方案对于人类来说简单易读易理解，但对于计算机来说很难处理，因为它们不得不明确地对于算术操作去比较幅度和符号。
  • 二进制反码(ones complement)同样，符号位中1代表负数0代表正数。正数值能够直接从数位中读取。然而，负数值不行，首先要将整个数都取反。在二进制反码中，取反的意思就是将所有位的0和1反转。为了找出一个负数的值，你必须先将它们的位都转回来。这个系统对于计算机来说更好一些，但仍然还有一些在加法上问题，以及就像符号和幅度表达的方法一样，对于两个这样的值会造成歧义：正0和负0。
  • 二进制补码(twos complement)符号位中1作为负数0作为正数。可以从正数值中直接从数位中读取大小，但无法从负数中的数位中直接读取。首先也需要将所有数位反转。在二进制补码中，反转操作意味着所有数位0和1反转，然后再加上1。这种方法对于机器来说能够非常好地工作，并且移出了会存在两个0的歧义。

（关于反码和补码为什么能在机器上很好地工作，本质上是一些数学性质上的优势，和本书给出的定义相反，从线性空间的角度去考量二进制补码和反码会显得非常直观与显然，关于这部分细节可以参考CSAPP的第二章相关部分——by译者）

正数通常在内部被表示为二进制补码，特别是在现代计算机中。就像前面提到的，二进制补码将正数编码为标准的二进制编码形式。正数值的范围取决于数位的位数。一个使用二进制补码的8位带符号整数有7个数位和1个符号位，7个数位能够表示从0到127。二进制补码将所有的负数值按照前面所述的方式编码，范围从-128到-1。也就是说，8位带符号整数能够表示-128到127的整数。

对于算术来说， 符号位放置在数据类型的最重要位中。 一般地，一个宽度为x的带符号补码能够表示的数范围为−2x−1到2x−1−1。下面的表显示了不同典型宽度补码能表示的数的范围。

8位 16位 32位 64位
最大值(带符号) -128 -32768 -2147483648 -9223372036854775808
最小值(带符号) 127 32767 2147483647 9223372036854775807
最大值(无符号) 0 0 0 0
最大值(无符号) 255 65535 4294967295 18446744073709551615

就先前面所述的，补码将所有数位反转并加1，下面的表给出了-15的补码表示：

1
0000 1111 15的标准二进制表示1111 0000 反转所有的位0000 0001 加11111 0001 -15的二进制补码1101 0110 一个不知道具体值的负数的二进制补码0010 1001 反转所有位0000 0001 加10010 1010 42的二进制形式，因此最初的值是-42
位的次序

在现代架构中，有两种将数位字节排序的约定：大端(big endian)和小端(little endian)。这些约定会使用于大于1个字节的数据类型，例如short和int型。在大端架构中，字节在内存中从最大位的字节开始到最小位的字节结束。小端在内存中的排布方式相反。例如，你有一个4位的整数，它的值位1234。在二进制中，它的值是11000000111001。这个值位于内存地址500的位置。在大端机器中，它会在内存中如此放置：

1
2
3
4
地址 500: 00000000
地址 501: 00000000
地址 502: 00110000
地址 503: 00111001

在小端机器中，它会这样放置：

1
2
3
4
地址 500: 00111001
地址 501: 00110000
地址 502: 00000000
地址 503: 00000000

因特尔机器是小端方式的，但是RISC机器，例如SPARC是大端方式的。一些机器能够同时应对两种约定。

常见的实现

从实践的角度讲，对于现代的，32位补码机器， 关于C的基本类型及其表示，你能说些什么 ？一般地，整数型不会带有填充位，所以你不需要考虑它。任何数都是用补码来表示的。一个字节会有8位的长度。字节的排序也有不同，在Intel机器上是小端方式，在RISC上是大端方式。

char类型默认为带符号类型并且占用1个字节。short类型占用2字节，int类型占用4字节。long型占4字节，long long型占8字节。在知道了整数是使用补码编码的，以及它们底层中占用的空间大小，得到它们能表示的最大和最小值就很简单了，下面的表总结了一些常见的整数类型数据在32位机器上所占空间大小与范围。

类型 长度(按位算) 最小值 最大值s
signed char 8 -128 127
unsigned char 8 0 255
short 16 -32,768 32,767
unsigned short 16 0 65,535
int 32 -2,147,483,648 2,147,483,647
unsigned int 32 0 4,294,967,295
long 32 -2,147,483,648 2,147,483,647
unsigned long 32 0 4,294,967,295
long long 64 -9,223,372,036,854,775,808 9,223,372,036,854,775,807
unsigned long long 64 0 18,446,744,073,709,551,615

当不久的将来64位机器更加普及时会怎样？ 下面的列表描述了一些目前正在使用或已经被提议的类型系统：

  • ILP32 int，long，指针为32位，和所有32位机器的标准一样
  • ILP32LL int， long，指针为32位，新的类型long long为64位。long long是C99标准中新增的，标准中规定它要有不小于64位大小，但它不悔更高任何语言的基础特性。
  • LP64 int， long，指针都为64位。int型更改为了64位， 这对该语言具有相当重要的意义。
  • ILP64 long和指针为64位，也就是指针和long类型从32位变成了64位
  • LLP64 指针和新的数据类型long long为64位。int和long型仍为32位。

下面的表简单总结了这些类型对应系统的大小：

类型 ILP32 ILP32LL LP64 ILP64 LLP64
char 8 8 8 8 8
short 16 16 16 16 16
int 32 32 32 64 32
long 32 32 64 64 64
long long N/A 64 64 64 64
pointer 32 32 64 64 64

如你所见，常见的数据类型的大小中，ILP32模型是32位平台上大多数编译器所遵循的。 LP64模型是为64位平台生成代码的编译器的真实标准。正如你在本章后面学到的，int类型是C语言的基本单元;许多东西都在幕后从它转换而来。由于int数据类型在表达式计算中非常依赖，LP64模型是64位系统的理想选择，因为它不会改变int数据类型;因此，它在很大程度上保留了预期的C类型转换行为。

7.2.4 算术边界条件

你已经了解了C的基本整数类型的最小和最大可能值是由它们在内存中的底层表示决定的。上面的表给出了32位补码体系结构的典型范围。 所以，现在你可以探索当你尝试跨越这些边界时会发生什么。对变量进行简单的算术运算，如加法、减法或乘法，可能会导致无法在该变量中保存值。看一下这个例子

1
unsigned int a;a=0xe0000020;a += 0x20000020；

你知道a可以没有任何问题地赋值为0xE0000020；无符号32位整数地最大值为4,294,967,295或者0xFFFFFFFF。然而，当0x20000020和0xE0000000相加后，理论上的结果值0x100000040无法被变量a容纳。当一个算术运算的结果值大于最大可能的表示数值时，我们就称他为数字溢出条件。

下面是一个有点不一样的例子：

1
2
3
unsigned int a;
a=0;
a-=1;

这个程序将a减去1，a的初始值为0，因此运算结果理论上为-1，但它不能被a容纳因为它小于了a的最小可能值0.这个结果被称为数字下溢条件。

注

数值溢出条件在安全编程文献中也称为数值溢出(numeric overflows)、算术溢出(arithmetic overflows)、整数溢出(integer overflows)或整数环绕(integer wrapping) 。数值下溢条件可称为数值下溢(numeric underflows)、算术下溢(arithmetic underflows)、整数下溢(integer underflows)或整数环绕。具体来说，可以使用术语“环绕一个值(wrapping around a value)”或“在0以下环绕(wrapping below zero)”。

(为什么叫wrapping，因为无论是underflow还是overflow都是从一个边界（上界或者下界）跳到另一个边界，就像一个闭环一样，至于为什么是闭环，主要是CPU的ALU在进行补码加法运算时会将溢出位舍去，详见CSAPP第二章的整数运算小节 —by译者)

尽管这些条件在实际代码中似乎并不常见或无关紧要，但它们实际上经常发生，而且从安全角度来看，它们的影响可能非常严重。算术运算的错误结果会破坏应用程序的完整性，并经常导致其安全性的损害。在代码块早期出现的数字溢出或下溢可能导致一系列微妙的级联错误(series of cascading faults);不仅单个算术操作的结果受到污染，而且后续使用该污染结果的每个操作都会引入一个攻击者可能会产生意外影响的点。

注

尽管数值环绕在大多数编程语言中很常见，但它在C/ C++程序中是一个特殊的问题，因为C要求程序员执行低级任务，而这些低级任务由更抽象的高级语言自动处理。这些任务，如动态内存分配和缓冲区长度跟踪，通常需要运行一些容易受到攻击的计算。攻击者通常通过操纵长度计算来利用算术边界条件，以便分配足够的内存。如果发生这种情况，程序以后就会冒在已分配空间的边界之外操作内存的风险，这通常会导致可利用的情况。另一种常见的攻击技术是绕过保护敏感操作(如内存副本)的长度检查。本章提供了几个例子，说明如何下溢和溢出条件导致可利用的漏洞。通常，审计人员在检查代码时应该注意算术边界条件，并确保考虑到这些细微的、层叠的缺陷可能带来的影响。

警告

我们在示例中尝试使用int和unsigned int类型，以避免代码受到C默认类型提升的影响。这个主题在本章后面“类型转换”中会提到，但现在，请注意，当你在C语言的算术表达式中使用char或short时，它会在算术执行之前被转换成int。

无符号整数边界

在C规范中，无符号整数被定义为服从模运算规则(参见“模运算”侧栏)。对于一个使用X位存储空间的无符号整数，该整数的算术运算以2X为模进行。例如，对8位无符号整数的运算以28或256为模进行。再看看这个简单的表达式 :

1
2
3
unsigned int a;
a=0xE0000020;
a+=0x20000020;

加法运算的模为232,或者4,294,967,296 (0x100000000)。加法的结果为0x40，也就是(0xE0000020 + 0x20000020)取0x100000000的模。

另一种概念化它的方法是将数字溢出结果的额外位视为截断。如果以二进制方式进行计算0xE0000020 + 0x20000020，将得到以下结果：

1
2
3
  1110 0000 0000 0000 0000 0000 0010 0000
+ 0010 0000 0000 0000 0000 0000 0010 0000
= 1 0000 0000 0000 0000 0000 0000 0100 0000

真实得到的a的结果是0x40，二进制形式为 0000 0000 0000 0000 0000 0000 0100 0000。

(其实Intel的CPU就是这么做的，ALU在做加法运算发生溢出时，溢出的进位会被舍掉，传到overflow flag里，详见CSAPP第二章—by译者)

模运算

模运算是计算机科学中广泛使用的一种运算系统。“X取Y的模”表示“X除以Y的余数”例如，100对11取余是1因为100除以11，结果是9余数是1。C中的模数运算符被写成%。因此在C中，表达式(100% % 11)的值为1，表达式(100 / 11)的值为9。

模运算对于确保数字被限制在一定范围内很有用，你经常在哈希表中看到它用于这个目的。解释一下，当X取Y的模，X和Y都是正数，结果的最大值是Y-1最小值是0。如果您有一个包含100个buckets的哈希表，并且你需要将一个哈希映射到其中一个bucket，那么你可以这样做：

1
2
3
4
struct bucket *buckets[100];
...
bucket = buckets[hash % 100];

对于模运算是如何工作的，可以见下面的简单循环：

1
2
3
for (i=0; i<20; i++)
	printf("%d ", i % 6);
printf("\n");

表达式(i% 6)本质上限定了i在0到5之间的范围。当程序运行时，它输出如下内容:

1
0 1 2 3 4 5 0 1 2 3 4 5 0 1 2 3 4 5 0 1

可以看到，当i从0上升到19时，i%6也上升了，但是每次它达到最大值5时，它就会返回到0。当你通过这个值向前移动时，你将环绕最大值5。如果向后移动这些值，则将从0”向下”环绕到最大值为5。

—- 以下内容接标题“模运算”之前—-

你可以看到它和加法的结果是一样的，但是没有最高位。这与机器层面的情况相差无几。例如，Intel架构有一个carry flag(CF)，它包含最高位。C语言没有允许访问这个标志的机制，但是根据底层架构，可以通过汇编代码来检查它。

下面是由于乘法而发生的数字溢出条件的示例 ：

1
2
3
unsigned int a;
a=0xe0000020;
a*= 0x42;

同样，以0x100000000为模进行算术运算。乘法的结果是0xC0000840，它是(0xE0000020 * 0x42)取0x100000000的模。下面是二进制表示：

1
2
3
          1110 0000 0000 0000 0000 0000 0010 0000
*         0000 0000 0000 0000 0000 0000 0100 0010
= 11 1001 1100 0000 0000 0000 0000 1000 0100 0000

实际上得到的结果是0xC0000840，它的二进制表示形式是1100 0000 0000 0000 0000。再一次，你可以看到不适合结果的较高位是如何被有效地截断的。在机器级别，通常可以检测整数乘法的溢出，并恢复乘法的高位。例如，在Intel上，imul指令在进行乘法运算时使用的目标对象大小是源操作数的两倍，如果乘法运算的结果需要大于源操作数的宽度，则imul指令将设置OF(overflow flag)和CF (carry flag)标志。一些代码甚至使用内联汇编来检查数值溢出(在本章后面的边栏“Intel上的乘法溢出”中讨论).

你已经看到了一些例子，它们说明了加法和乘法是如何导致算术溢出的。另一个可能导致溢出的操作符是左移，在本讨论中，它可以被认为是与2的乘法。它的行为与乘法非常相似，因此这里没有提供示例。

现在你可以来看一些与无符号整数算术溢出相关的安全问题了。下面的代码是最近在客户机代码中发现的可利用条件的经过清理、编辑的版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
u_char *make_table(unsigned int width, unsigned int height,
				u_char *init_row)
{
	unsigned int n;
	int i;
	u_char *buf;
	n = width * height;
	buf = (char *)malloc(n);
	if (!buf)
		return (NULL);
	for (i=0; i< height; i++)
		memcpy(&buf[i*width], init_row, width);
	return buf;
}

makr_table()函数的目的是获取宽度(width)，高度(height)，以及初始行(init_row)在内存中创建一个表格，每行初始化为和init_row相同的值。即假定用户能用width和height控制表格的维度。如果他们使用了一个非常大的维度，例如width设置为1,000,000，宽度设置为3,000，那么malloc()函数就会尝试申请3,000,000,000字节的内存空间。内存分配可能会失败，然后所调用的函数检测到错误以后会优雅地去处理它。然而，用户可以用它在width和height的相乘中造成算术溢出，只要将维度设置的足够大。潜在来说这种溢出已经可以被利用了，因为内存分配在width和height相乘后完成，而表格的初始化是在后面的for循环中进行的。因此如果我将width设置为0x40，height设置为0x1000001，乘法的结果就会是0x400000400，这个值对0x100000000的模是0x00000400，用十进制表示就是1024.所以1024个字节会被分配，但for循环会将init_row严格地进行1600万次复制。一个聪明的攻击者就能够通过进程运行时环境的底层细节来利用这种溢出获得整个应用程序的控制权。

现在再来看一个和上面例子相近的真实漏洞案例，这个例子发现于在OpenSSH 服务器。下面的代码来自OpenSSH 3.1问答认证(challenge-response authentication)代码：auth2-chall.c中的input_userauth_info_response()函数：

1
2
3
4
5
6
7
8
9
	u_int nresp;
...
	nresp = packet_get_int();
	if (nresp > 0) {
		response = xmalloc(nresp * sizeof(char*));
		for (i = 0; i < nresp; i++)
			response[i] = packet_get_string(NULL);
	}
	packet_check_eom()

无符号整数nresp是用户能够控制的，它的目的是告诉服务器有多少响应。它被用来分配response[]数组然后将这个网络数据填充进去。在response[]数组通过xmalloc()的调用分配后，resp会乘以sizeof(char*)，也就是4个字节。如果用户将nresp设置得足够大，算术溢出就会发生，然后乘法的结果就可能会变成一个较小的数。例如，如果nresp的值是0x40000020，乘法的结果就会是128(0x80),因此，0x80个字节就会被分配，但for循环会尝试将0x40000020个字符从packet取出然后送到response[]里！这就是一个可以远程利用的危险漏洞。

现在将注意力集中到算数下溢上。对于无符号整数，做减法时可能会导致一个值从最小可表示值0环绕。由于取模的过程，最终下溢的结果会是一个非常大的正数。下面是一个简短的例子：

1
2
unsigned int a;
a=0x10;a-=0x30;

我们来看一下二进制下的计算:

1
2
3
  0000 0000 0000 0000 0000 0000 0001 0000
- 0000 0000 0000 0000 0000 0000 0011 0000
= 1111 1111 1111 1111 1111 1111 1110 0000

最终a的结果会是0xffffffe0，在二进制补码的表示下是一个负数-0x20。但在模运算的前提下，如果你将数值移动超过了最大可能的值，那你就会在0处环绕。类似的情况也会在你低于最小值时发生：你将会环绕到最大的数值上。由于a是一个unsigned int型，因此它的值在减法后就会是0xffffffe0而不是-0x20。限免的代码是一个关于无符号整数算数下溢的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct header {
	unsigned int length;
	unsigned int message_type;
};
char *read_packet(int sockfd)
{
	int n;
	unsigned int length;
	struct header hdr;
	static char buffer[1024];
	if(full_read(sockfd, (void *)&hdr, sizeof(hdr))<=0){
		error("full_read: %m");
		return NULL;
	}
	length = ntohl(hdr.length); //这里length是加粗
	if(length > (1024 + sizeof (struct header) - 1)){
        error("not enough room in buffer\n");
		return NULL;
	}
	if(full_read(sockfd, buffer,
			length sizeof(struct header))<=0) //这里length加粗
	{
		error("read: %m");
		return NULL;
	}
	buffer[sizeof(buffer)-1] = '\0';
	return strdup(buffer);
}

这份代码从网络中读入packet的header然后取出它的32位长度写入length变量中。length变量表示packet所占的总字节数，因此程序会先检查packet数据部分是否长于1024个字节以防止溢出。然后它尝试通过将(length sizeof(struct header))个字节读入缓冲区，从网络中读取packet的其余部分。这是有意义的，因为代码希望读取packet的数据部分，即总长度减去头的长度。

有漏洞的地方在于如果用户将长度设置为小于sizeof(struct header)的值，那么减去(length sizeof(struct header))就会造成整数下溢，最后将一个很大的size参数掺入full_read()。这个错误可能造成缓冲区溢出，因为在那个时候，read()可能会一直将数据复制到缓冲区知道连接关闭时，这样就可能允许攻击者获得进程的控制权。

Intel中的乘法溢出

一般地，处理器会在发生整数溢出时探测到它然后提供处理机制；然而，它们几乎没有用在错误检查上并且一般这种机制C语言也没有访问权限。例如，Intel处理器会在乘法发生溢出时将overflow flag(OF)的值保存在EFLAGS寄存器中，但C成语言如果不使用内部汇编代码的话就无法检查这个flag。有时这样做是出于安全原因，例如在Windows操作系统中处理MSRPC请求的NDR解组例程。下面的代码来自rpcrt4.dll，会在从RPC请求中各种数据类型的解组中调用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
sub_77D6B6D4 proc near
var_of = dword ptr -4
arg_count = dword ptr 8
arg_length = dword ptr 0Ch
push ebp
mov ebp, esp
push ecx
and [ebp+var_of], 0
		; set overflow flag to 0
push esi
mov esi, [ebp+arg_length]
imul esi, [ebp+arg_count]
		; multiply length * count
jno short check_of // 这一行是加粗，第一次检查
mov [ebp+var_of], 1
		; if of set, set out flag
check_of:
cmp [ebp+var_of], 0
jnz short raise_ex
		; must not overflow
cmp esi, 7FFFFFFFh //第二次检查
jbe short return
		; must be a positive int
raise_ex:
push 6C6h
		; exception
call RpcRaiseException
return:
mov eax, esi
		; return result
pop esi
leave
retn 8

你能看到这个函数会将所提供的元素数量和每个元素的大小相乘，这个过程中做了两次检查。第一次是它使用jno检查overflow flag来保证乘法没有导致溢出。然后它确保了结果值的大小小于或者等于带符号整数能表示的最大值，也就是0x7FFFFFFF，二者只要有其中之一检查失败，函数就会抛出异常。

带符号整数边界

带符号整数略有不同。根据C语言特性，带符号整数的算术溢出或下溢的结果是实现定义的，可能包含机器陷阱或故障(machine trap or fault)。然而在大多数常见架构中，有符号算术溢出的结果定义良好且可预测，不会导致任何类型的异常。这些边界行为是补码算法在硬件上实现的自然结果，在主流机器上应该是一致的。

如果你还记得的话，可以用二进制补码表示的最大带符号整数的正值是，除有效位为0外，所有位都被设为1。这是因为最大的位表示该数字的符号，而该位中的值为1表示该数字为负数。当对有符号整数的操作导致算术溢出或下溢时，结果值“包围符号边界”并通常导致符号更改。例如，在32位整数中，值0x7FFFFFFF是一个大的正数。向其添加1将产生结果0x80000000，这是一个很大的负数。看看另一个简单的例子：

1
2
3
int a;
a=0x7FFFFFF0;
a+=0x100

加法的结果是-0x7fffff10, 或者 -2,147,483,408。来看一下它的二进制加法过程：

1
2
3
  0111 1111 1111 1111 1111 1111 1111 0000
+ 0000 0000 0000 0000 0000 0001 0000 0000
= 1000 0000 0000 0000 0000 0000 1111 0000

a的结果值是0x800000f0，它是正确的结果，但由于整数是用二进制补码来表示的，实际的值就会被表示为-0x7fffff10。在这个情况下，一个很大的正数加上一个很小的正数得到了一个很大的负数。

使用带符号加法，你可以通过使正数绕到0x80000000周围变成负数来溢出符号边界。你还可以通过使一个负数绕到0x80000000以下并变成正数来降低符号边界。负数的减法和加法是一样的，所以你可以把它们分析成本质上是相同的运算。乘法和移位过程中也可能出现溢出，对其结果进行分类就不那么容易了。从本质上说，这些位元可能会下落;如果结果的符号位中有1位，结果就是负的。否则,它不是。乍一看，涉及乘法的算术溢出似乎有点棘手，但攻击者通常可以让它们返回有用的目标值。

注

在本章中，read()函数用于演示与整数相关的各种形式的缺陷。为了清晰起见，这有点过于简化了，因为许多现代系统在系统调用级别验证read()的长度参数。这些系统(包括BSDs和更新的Linux 2.6内核)检查这个参数是否小于或等于相应大小的有符号整数的最大值，从而最小化内存损坏的风险。

很多在计算中未预料到的符号改变可以导致代码中微妙的可利用漏洞。这些变化可能曹正程序错误地计算所要求的空间，导致出现和上面无符号整数越过边界相似的情况。这种性质的错误通常发生在对直接从外部源(如网络数据或文件)获取的整数执行算术运算的应用程序中。下面的代码就是一个简单的例子，它展示了应用程序越过符号边界可能造成的影响：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
char *read_data(int sockfd)
{
	char *buf;
	int length = network_get_int(sockfd);
	if(!(buf = (char *)malloc(MAXCHARS)))
		die("malloc: %m");
	if(length < 0 || length + 1 >= MAXCHARS){
		free(buf);
		die("bad length: %d", value);
	}
	if(read(sockfd, buf, length) <= 0){
		free(buf);
        die("read: %m");
	}
	buf[value] = '\0';
	return buf;
}

这个例子从网络中读入一个整数然后首先理智地做了一些检查。首先，检查了长度来保证它是否大于等于0，也就是是否为正数。然后检查长度来保证它是否小于MAXCHAS。然而，在代码的第二部分检查中，length变量被加了1.这就给攻击向量开了一扇门：0x7FFFFFFF会通过第一道检查（因为它大于0）然后进入第二道检查后，0x7FFFFFFF + 1是0x80000000，也就是一个负数，read()然后就可能在使用了一个有效的没有限制长度的参数下调用，从而导致潜在的缓冲区溢出情况。

在对待带符号整数时，这样的错误会很容易犯，而且发现它同样具有挑战性。允许用户直接指定整数的协议特别容易出现这种类型的漏洞。为了在实践中检验这一点，我们来看看一个执行不安全计算的真实应用程序。以下漏洞是OpenSSL 0.9.6代码基中与处理抽象语法符号(Abstract Syntax Notation ASN.1)编码数据相关的漏洞。(ASN.1是一种用于描述在计算机之间发送的任意信息的语言，这些信息使用它的基本编码规则BER进行编码。)这种编码是这种性质的漏洞的完美候选，因为该协议显式地处理由不受信任的客户机提供的32位整数。下面代码取自crypto/asn1/a_d2i_fp.c的 ASN1_d2i_fp()函数，该函数负责从IO (BIO)缓冲流中读取ASN.1对象。为简洁起见，对该代码进行了编辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
c.inf=ASN1_get_object(&(c.p),&(c.slen),&(c.tag),&(c.xclass),
				len-off);
...
{
	/* suck in c.slen bytes of data */
	want=(int)c.slen;
	if (want > (len-off))
	{
		want-=(len-off);
    	if (!BUF_MEM_grow(b,len+want))
		{
			ASN1err(ASN1_F_ASN1_D2I_BIO,
				ERR_R_MALLOC_FAILURE);
			goto err;
		}
		i=want;
        // 这里所有want都加粗了

这份代码在一个获取ASN.1对象的循环中被调用。ASN1_get_object()函数读取下一个ASN.1对象指定长度的对象头部。这个长度被放置在c.slen里，是一个带符号整数，然后被传入want中ASN.1对象函数确保了这个值非负，因此c,slen的最大值可以是0x7FFFFFFF。在这种情况下，len就是内存中早已读入的数据数量，off是该数据到被解析对象的偏移量。因此，len-off就是被读入内存但还未被解析的数据量。如果代码发现对象大小大于可用的未解析数据大小，则决定分配更多空间并读入对象的其余部分。

BUF_MEM_grow()函数用来在内存缓冲区b中分配所要求的内存空间。它第二个变量是大小参数。这里的问题就是，len+want表达式用于第二个参数就可能导致溢出。比如假设len是200字节，off是50字节，攻击者经对象大小设置为0x7FFFFFFF，这将会传给want。 0x7FFFFFFF比在内存中的150个字节数据要大得多，因此会进入分配内存的代码。want会被减去150个已经读入的数据大小，然后得到值0x7FFFFF69，然后BUF_MEM_grow()的调用会请求len+want个字节的数据，或者说x7FFFFF69 + 200，也就是0x80000031，这个数是一个非常大的负数。

在内部，BUF_MEM_grow()函数进行比较，检查长度参数与之前分配的空间大小。因为负数小于它已经分配的内存量，所以它假定一切正常。因此，重新分配将被绕过，任意数量的数据可能被复制到分配的堆数据中，这会带来严重的后果。

7.2.5 类型转换

C语言在处理不同数据类型的交互上非常灵活。例如，通过一些强制类型转换，可以轻松地将无符号字符与有符号长整数相乘，将其添加到字符指针中，然后将结果传递给需要指向结构的指针的函数。程序员已经习惯了这种灵活性，因此他们倾向于混合数据类型，而不太关心幕后发生的事情。为了处理这种灵活性，当编译器需要将一种类型的对象转换为另一种类型时，它将执行所谓的类型转换。类型转换有两种形式:显式类型转换，程序员通过强制转换显式指示编译器从一种类型转换为另一种类型;隐式类型转换，编译器对变量进行“隐藏”转换，以使程序按预期运行。

注

你可能会看到在编程语言文献中称为“类型强制转换”(type coercions)的类型转换;这两个术语是同义的。

当你第一次了解一个典型的C程序中在幕后发生了多少隐式转换时，通常会感到惊讶。这些自动类型转换统称为默认类型转换，这会在当程序员执行看似简单的任务(如进行函数调用或比较两个数字)时，几乎不可思议地发生。

类型转换产生的漏洞通常很有趣，因为它们很微妙，很难在源代码中定位，而且它们常常导致这样的情况:关键远程漏洞的补丁就像将char更改为unsigned char一样简单。控制这些转换的规则看起来很微妙，你很容易认为你已经牢牢掌握了它们，而忽略了在分析或编写代码时造成巨大差异的一个重要的细微差别。

我们先部不要直接跳到已知的漏洞类别中，首先看看C编译器是如何在较低的级别上执行类型转换的，然后详细研究C的规则，以了解发生转换的所有情况。本节相当长，因为在有信心分析C的类型转换的基础之前，你必须涵了解很多内容。然而，这方面的语言是非常微妙的，它绝对值得花时间来获得一个坚实的基本规则的理解;你可以利用这种理解来发现大多数程序员甚至在概念级别上都没有意识到的漏洞。

概述

当面对协调两种不同类型的普遍问题时，C尽量避免让程序员感到意外。编译器遵循一组规则，这些规则试图封装关于如何管理混合不同类型的“常识”，通常，这些程序结果是正确的，且简单地执行程序员想要的操作。也就是说，应用这些规则通常会导致令人惊讶的、意想不到的行为。此外，如你所料，这些意外行为往往会带来可怕的安全后果。

在下一节中，我们将从探讨转换规则开始，即C在类型之间转换时使用的一般规则。它们指示机器如何在位级从一种类型转换为另一种类型。在您你很好地掌握了C如何在机器级别上在不同类型之间转换之后，你将研究编译器如何选择在C表达式上下文中应用哪种类型转换，这涉及到三个重要的概念:简单转换(simple conversions)、整数提升(integer promotions)和通常的算术转换(arithmetic conversions)。

注

虽然浮点数和指针等非整型类型有一定的覆盖范围，但本文主要讨论的是C如何操作整数，因为这些转换被广泛误解，并且对安全性分析至关重要。

转换规则

下面的规则描述了C如何从一种类型转换为另一种类型，但它们不描述何时执行转换或为什么执行转换。

注

下面的内容是特定于二进制补码实现的，代表了C规范中规则的精炼和实用版本。

整数类型：保值

在整数类型的转换中，一个重要的术语就是保值转换(value-preserving conversion)。

简单来说，如果新的类型能够表示所有旧类型可能的值，那么这种转换就成为保值的。在这种情况下，转换的结果不会导致值发生任何变化或者丢失。例如，如果一个unsigned char转换为int，这个转换就是保值的，因为整型能够表示无符号字符型的任意值。你可以在后面的表中对它进行验证。假设你考虑的是使用二进制补码的机器，那么一个8位的unsigned char能够表示0-255的任意值。一个32位的int型能够表示 -2147483648和 2147483647之间的任意值。因此没有一个unsigned char能表示的数字是int不能表示的。

相应地，在变值转换(value-changing conversion)中，旧地类型可能包含了新类型无法表示的值。例如，如果你将int转换为unsigned int，你就创造了这样一个棘手的情况。unsigned int在32位机器上的范围是0-4294967295,int的范围是-2147483648-2147483647.unsigned int无法表示任何int能表示的负数。

根据C标准，一些变值转换的结果有实现定义。这仅适用于具有带符号目标类型的值更改转换;对无符号类型的变值转换进行了定义，并且在所有实现中保持一致。(如果你还记得边界条件的讨论，这是因为无符号算术被定义为模运算系统。)二进制补码机遵循相同的基本行为，因此你可以相当有把握地解释它们如何执行对带符号目标类型的值更改转换。

整数类型：扩展

当你将一个较窄类型转换为另一个更宽的类型时，机器会按位将旧的变量复制到新的变量，然后将其他的高位设为0或者1.如果源类型是无符号的，机器就会使用零扩展(zero extension)，也就是在宽类型中将剩余高位设为0.如果源类型是带符号的，机器就会使用符号位扩展(sign extension)，也就是将宽类型剩余未使用位设为源类型中符号位的值。

警告

扩展过程会出现一些没有预料的实现：如果一个较窄的带符号类型，例如signed char，转换为一个更宽的无符号类型，例如unsigned int，那么符号位扩展仍然会发生。

图6-1展示了一个值为5的unsigned char类型保值转换为signed int型的过程

6-1

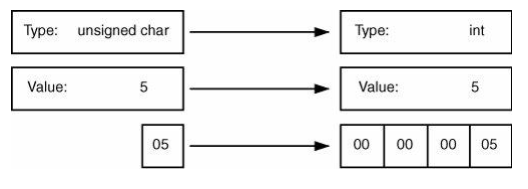
字符被放置到整数中，值被保留。在位模式级别，这只涉及零扩展:清除高位并将最低有效字节(least significant byte，LSB)移动到新对象的最低有效字节。

现在考虑一下signed char转换为int。int能表示所有signed char能表示的值，因此这个转换仍然是保值的，图6-2展示了在位级别的转换过程。

6-2

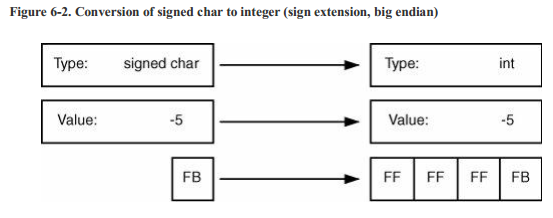
这个情况稍微会有些不同，因为值是相同的，但转变过程更复杂了一点。-5在signed char中位级别的表示为1111 1011。在int中，-5的位级表达为1111 1111 1111 1111 1111 1111 1111 1011.为了实现这个转换，编译器会生成汇编代码来执行符号位扩展。在图6-2中你能看到符号位在signed char中为1，因此为了保值，符号位就会被复制到其他int型中剩下的24位里。

前面的例子是保值转换。现在考虑一下变质扩展转换。如果你想要将一个值为-5的signed char转换为unsigned int。由于源类型是带符号的，因此符号位扩展就会执行，见图6-3：

6-3

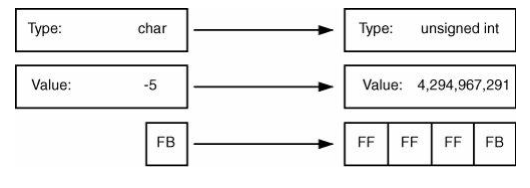
正如前面所提到的，这个结果可能会震惊到开发者。你可以在本章后面“符号位扩展”小节中看到与之相关的安全影响。这种转换是变值的，因为一个unsigned int无法表示一个小于0的值。

整数类型：收缩

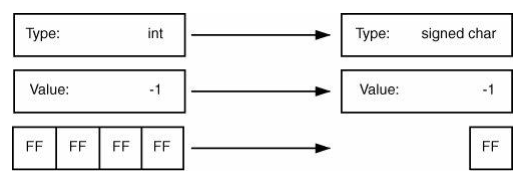
当将一个宽类型转换为窄类型时，机器只会使用一种机器：截断(truncation)。宽类型中与窄类型不匹配的位会被全部舍去。图6-4和图6-5展示了两个收缩转换。注意，所有的收缩转换都是变值转换，因为转换过程中精度丢失了。

6-4

图6-5:

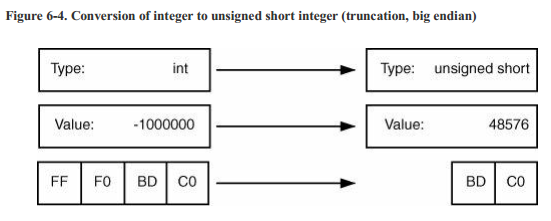
6-5

整数类型：带符号与无符号

最后我们要考虑这样的整数转换：如果转换在相同宽度的带符号和无符号数之间发生，那么在位级别上什么都不会发生。这样的转换是变值的。例如，如果你有一个signed int型的-1，在二进制的表示为：1111 1111 1111 1111 1111 1111 1111 1111。

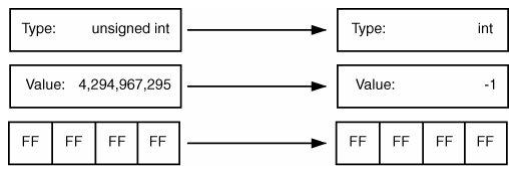
如果将具有相同位级别的这个数看作unsigned int，那么它的值就是4,294,967,295。这个过程在图6-6中有总结。 从unsigned int到int的转换在技术上可能是实现定义的，但其工作方式相同:保留位模式，值在新类型的上下文中进行解释

6-6

图6-7：

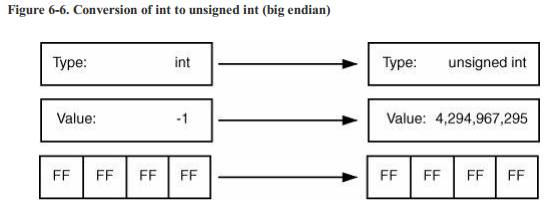
6-7

整数类型转换总结：

对于整数类型转换，这里有一些实用的规则：

  • 从窄的带符号类型转换为宽的无符号类型，编译器会生成汇编指令执行符号位扩展，对象的值可能会改变。
  • 从窄的带符号类型转换为宽的带符号类型，编译器会生成汇编指令执行符号位扩展，对象的值不变
  • 从窄的无符号类型转换为宽的类型，编译器会生成汇编指令执行零扩展，对象的值不变
  • 从宽类型转换为窄号类型，编译器会生成汇编指令执行截断，对象的值可能改变
  • 相同宽度无符号类型和带符号类型之间的转换，编译器实际上不会做任何事，在位模式下是相同的，但对象的值可能会改变

下面的表总结了不同整数类型在C语言的二进制补码实现下转换时进行的操作。在接下来的章节中，这个表可以当作类型转换发生时一个有用的参考文献。表中左边是源类型，顶部代表目标类型。

signed char unsigned char short int unsigned short int signed int unsigned int
signed char 相容类型 变值 保值 变值 保值 变值
位模式不变 符号位扩展 符号位扩展 符号位扩展 符号位扩展
unsigned char 变值 相容类型 保值 保值 保值 保值
位模式不变 零扩展 零扩展 零扩展 零扩展
short int 变值 变值 相容类型 变值 变值 变值
截断 截断 位模式不变 符号位扩展 符号位扩展
unsigned short int 变值 变值 变值 相容类型 保值 保值
截断 截断 截断 零扩展 零扩展
signed int 变值 变值 变值 变值 相容类型 变值
截断 截断 截断 截断 位模式不变
unsigned int 变值 变值 变值 变值 变值 相容类型
截断 截断 截断 截断 位模式不变

浮点型和复数型

尽管由浮点数算术导致的漏洞并没有广泛地被挖出来，但造成漏洞这一件事是确实可能的。在财务软件中肯定会出现与浮点类型转换或表示问题相关的微妙错误。本章对浮点类型的讨论相当简短。有关更多信息，请参阅C标准文档和前面提到的C编程参考资料。

对于真正的浮点类型和整数类型之间的转换，C标准的规则为实现定义的行为留下了很大的空间。在从实类型到整数类型的转换中，将丢弃数字的小数部分。如果整数类型不能表示浮点数的整数部分，则结果是未定义的。类似地，从整数类型到实类型的转换也会尽可能地转移值。如果实类型不能表示该整数的值，但可以接近，则编译器将按照实现定义的方式将该整数四舍五入到下一个最大值或最小值。如果整数超出实类型的范围，则结果是未定义的。

不同精度的浮点类型之间的转换使用类似的逻辑处理。精度提升(promotion)不会引起值的变化。在导致值更改的精度下降(demotion)期间，编译器可以自由地使用实现定义的方式对数字进行四舍五入(如果可能的话)。如果由于目标类型的范围而无法四舍五入，则结果是未定义的。

其他类型

除了整数和浮点数之外，C语言中还有无数其他类型，包括指针、布尔型、结构体、联合体、函数、数组、枚举类型等等。在大多数情况下，从安全的角度来看，这些类型之间的转换并不十分关键，因此本章不会详细介绍它们。

指针运算会在本章中的“指针运算”小节中进行详细介绍。指针类型转换很大程度上取决于底层机器的架构，很多的类型转换都是实现定义的。实质上，程序员能够将指针和整型来回转换，将指针从一种类型转换为其他类型。其结果是实现定义的， 程序员需要认识到对齐限制和其他底层细节。

简单转换

现在你对C语言将一个整数类型转换为其他类型已经了解了，现在你可以来看一下这些类型转换发生时的情况了。简单转换(simple conversions)是一种C语言表达式，它直接使用前面提到的转换规则。

强制类型转换(casts)

强制类型转换(typecasts)是C语言让程序员进行显式类型转换的机制，就像下面的例子一样:

1
(unsigned char) bob

不管bob是什么，这个表达式都会将它转换为unsigned char类型。表达式的结果类型是unsigned char。

赋值

简单类型的转换也会在赋值运算符中发生。编译器一定会将右部的类型转换为左部的类型，就像下面例子所显示的：

1
2
3
short int fred;
int bob = -10;
fred = bob;

对于这两个赋值运算，编译器一定会将右部的类型转换为左部的类型。转换规则告诉你，从int类型的bob转换为short int型的fred会导致截断。

函数调用：原型(prototype)

C语言有两种风格的函数声明：旧的K&R风格，也就是参数类型在函数声明中没有具体说明。在ANSI风格中， 函数原型的使用仍然是可选的，但它很常见，在ANSI风格下，你会见到一些像这样的东西：

1
2
3
4
5
6
7
8
int dostuff(int jim, unsigned char bob);
void func(void)
{
    char a=42;
    unsigned short b=43;
    long long int c;
    c=dostuff(a, b);
}

函数dostuff()的声明中含有告诉编译器参数个数的原型。 经验法则是，如果函数有原型，则使用前面记录的规则以简单的方式转换类型。 如果函数没有原型， 就会出现所谓的默认参数提升(default argument promotions)(在整数提升中会提到)。

前面的例子中一个字符型（a）被转换为了int型(jim)，一个unsigned short型(b)被转换为了unsigned char(bob)，一个int型(do_stuff()的返回值)被转换成了long long int(c)。

函数调用：返回

return 将其操作数转换为封闭函数定义中指定的类型。例如，在下面的例子中，int类型a通过return被转换为了char类型：

1
2
3
4
5
char func(void)
{
    int a=42;
    return a;
}
整数提升(integer promotions)

整数提升详细说明了C语言如何将一个窄的整数类型，例如char或者short转换为int型（或者不常见的情况，转换为unsignd int)。由于下面的两种原因会使用这种向上的转换(up-conversion)，或者提升：

  • 很多C语言的运算符要求操作对象为int或者unsigned int类型。对于这些运算符，C会使用整数提升规则将窄类型操作对象转换为int或者unsigned int。
  • 整数提升是C语言中处理算术表达式中很重要的规则，它也被称为常规算术转换规则 (usual arithmetic conversions)。对于涉及整数的算术表达式，整数提升通常应用于操作数两边。
注

你可能会在其他文献中交替见到“整数提升(integer promotion)”和“整型提升(integral promotion)”，它们是相同的术语。

从C语言便准中能得到一个有用的概念：每个整数型数据都有一个叫整数转换等级(integer conversion rank)的东西。这些等级将整数类型数据做了一个等级的排序，通过它们的宽度从低到高。每种类型的带符号和无符号种类级别是相同的。 下面的列表按从高到低的等级转换对整数类型进行排序。对于其他整数类型，C标准也会设置等级，但是这个列表应该足以满足本文的讨论：

  • long long int, unsigned long long int
  • long int, unsigned long int
  • unsigned int, int
  • unsigned short,short
  • char, unsigned char, signed char
  • _Bool

基本来说， 在C中可以使用int或unsigned int的任何地方，也可以使用具有较低整数转换等级的任何整型。这意味着你可以使用更小的类型，比如char和short int，来代替C表达式中的int。你也可以使用类型为_Bool、int、signed int或unsigned int的位字段。位字段不被赋予整数转换等级，但它们被视为比它们相应的基类型更窄的类型。 这是有意义的，因为int的位字段通常比int小，最宽的情况下和int的宽度相同。

如果将整数提升应用于变量，会发生什么?首先，如果变量不是整数类型或位字段，提升过程不会执行任何操作。第二，如果变量是整数类型，但是它的整数转换级别大于或等于int类型，提升过程也不做任何事情。因此，int、unsigned int、long int、指针和浮点数不会因整数提升而改变。

因此，整数提升负责获取更窄的整型类型或位字段，并将其提升为整型或无符号整型。否则，将执行一个到unsigned int的保值转换。

在实际应用中，这意味着几乎所有东西都能被转换为int，因为int可以保存所有较小类型的最小值和最大值。唯一可能提升为无符号整型的类型是具有32位的无符号整型位字段，或者某些特定于实现的扩展整型类型。

关于过去版本的注解

C89标准对C类型转换规则进行了重要的修改。在C语言的K&R时代，整数提升是保符号(unsigned-preserving)的，而不是保值的。因此，在当前的C规则中，如果较窄的无符号整数类型(如unsigned char)被提升为较宽的有符号整数(如int)，则值转换规定新类型为有符号整数。在旧规则中，提升将保留无符号性，因此结果类型将是unsigned int，这改变了许多有符号/无符号比较的行为，这些比较涉及到比int窄的类型提升。

整数提升的总结

基本上的规则如下：如果一个整数类型比int要窄，那么证书体系基本上都会将它们转换为int。下面的表总结了几个常见类型的整数提升结果：

源类型 结果类型 转换原理
unsigned char int 提升；源类型等级低于int等级
char int 提升；源类型等级低于int等级
short int 提升；源类型等级低于int等级
unsigned short int 提升；源类型等级低于int等级
unsigned int:24 int 提升；unsigned int的位字段
unsigned int:32 unsigned int 提升；unsigned int的位字段
int int 不提升，源类型等级等于int等级
unsigned int unsigned int 不提升，源类型等级等于int等级
long int long int 不提升，源类型等级大于int等级
float float 不提升，源类型不是整数类型
char* char* 不提升，源类型不是整数类型
整数提升应用

现在你理解整数提升了，下面的小节会探讨它们会在C语言哪些地方被使用。

一元算符 +

一元算符 +会对其操作数执行整数提升。例如，如果变量bob的类型是char，那么(+bob)的结果类型为int，尽管(bob)表达式的结果类型为char。

一元算符 -

一元算符-会对其操作数先执行整数提升再取负数。 无论提升后的操作数是否有符号，都会执行二进制补码的取负，这涉及到位的反转，然后加一。 (一个数取负，只要把数的补码表示再取一次补码就可以了 —by译者)

Leblancian悖论

David Leblanc是一位专业的研究员和审计者，也是世界上C/C++的顶级专家之一。 他记录了在与同事Atin Bansal一起开发SafeInt类时发现的两个补码运算的一个迷人的细微差别(http://msdn.microsoft.com/library/en-us/dncode/html/secure01142004.asp)。将两个补码数相减，会执行各位取反然后加1。假设一个32位的带符号数据类型，那么0x80000000取反是什么？

你将所有位取反后，得到了0x7fffffff，然后加上1，你得到了0x80000000。因此这个数的取负就是它本身！

当开发人员使用负整数表示一组特殊的数字或尝试取整数的绝对值时，这种特性就会发挥作用。下面的代码让一个负索引指定一个辅助哈希表。除非攻击者能够指定索引为0x80000000，否则这种方法可以正常工作。对数字进行取负不会导致值发生变化，并且0x80000000 % 1000是-648，这会导致数组之前的内存被修改。

1
2
3
4
5
6
7
8
9
10
11
int bank1[1000], bank2[1000];
...
void hashbank(int index, int value)
{
	int *bank = bank1;
	if (index<0) {
		bank = bank2;
		index = -index;
	}
	bank[index % 1000] = value;
}

译者注：

补码在数学性质上是单满映射，也就是在能够表示的范围之内，一个数的和它的二进制补码是一一对应的，那么为什么会出现上述的悖论(一个数的补码负数是本身)呢？本质上就是0x80000000是int型能表示的最小值，而int型能表示的最大值是最小值的绝对值减一，也就是说int是无法表示-0x80000000的，它理论值是-INT_MIN-1，即INT_MAX+1，但在int里这个数就越界了，然后就从INT_MAXoverflow回了INT_MIN。

一元算符 ~

一元算符~会在进行整数提升之后将操作数取反码。 对于补码实现，这有效地对有符号和无符号操作数执行相同的操作:将位反转。

移位算符

移位算符>>和<< 改变变量的位模式。整数提升会应用到这两个算符中，结果类型等于算符左边操作数提升后的类型，就像下面例子一样：

1
2
3
4
char a = 1;
char c = 16;
int bob;
bob = a << c;

a会被转成整数，c也会被转成整数。提升后的左边操作数是int型，因此表达式的结果类型是int。a的整数表达就是原来的值往左移16位。

switch语句

整数提升也会用在switch语句中。switch语句的表达式一般会像这样：

1
2
3
4
5
6
7
switch (controlling expression)
{
    case (constant integer expression): body;
    	break;
    default: body;
    	break;
}

整数提升以以下方式使用:首先，它们应用于控制表达式，以便表达式具有提升类型。然后，将所有整型常量转换为控制表达式提升的类型。

函数调用

使用K&R语义的旧C语言程序在其函数声明中没有指定参数的数据类型。当在没有原型的情况下调用函数时，编译器必须执行称为默认参数提升(default argument promotions)的操作。基本上，整数提升应用于每个函数参数，任何浮点类型的参数都转换为double类型的参数。考虑以下示例：

1
2
3
4
5
6
7
8
9
10
int jim(bob)
char bob;
{
	printf("bob=%d\n", bob);
}
int main(int argc, char **argv)
{
	char a=5;
	jim(a);
}

在这个例子中，a的拷贝值被传入了jim()函数。char类型首先会被整数提升整数类型，然后这个整数会被传入jim()函数。 编译器为jim()函数发出的代码需要一个整型参数，它执行将该整型直接转换回bob变量的char格式。

常规算术转换

在许多情况下，C应该接受两个可能具有不同类型的操作数，并执行一些涉及这两个操作数的算术运算。C标准给出了一种通用算法，用于将两种类型协调为兼容类型。 这个方法称为常规算术转换(usual arithmetic conversions)。

规则1：浮点优先

浮点数要优先于整数类型，也就是如果一个变量在算术表达式中是浮点数类型，那么其他类型就会被转换为浮点型。如果一个浮点型比其他的类型精度低，那么这个浮点型会被提升为精度更高的类型。

规则2：应用整数提升

如果两个操作数都不是浮点型，那么回到整数类型的规则。首先，整数提升会应用到两边的操作数。这是拼图中极其重要的一块！如果你回顾前面的章节，这个规则表示任何小于int的整数类型都会被转换为int，与int有相同宽度或者更宽的会被放到一边。下面是一个简单的例子：

1
2
3
unsigned char jim = 255;
unsigned char bob = 255;
if ((jim + bob) > 300) do_something();

在这个表达式中，运算符+会对操作数使用常规算术转换，结果类型会是一个int型，并且记录加法的值(510)。因此，do_something会被调用，尽管这个表达式看起来会导致溢出。 总而言之:只要算术涉及小于整数的类型，就会在幕后将窄类型提升为整数。这里有另一个简单的例子：

1
2
unsigned short a=1;
if ((a-5) < 0) do_something();

从直观上看如果你有一个值为1的unsigned short，减去5以后会在0处下溢到一个很大的值。然而，如果你测试这段代码，你将会看到do_something()被调用了因为减法算符两边的操作数在比较前都被提升到了int型。因此a被从unsigned short转换成了int，然后一个int类型的的数减去了5，结果是-4。这对int是合法值，因此比较表达式的结果为真。请注意如果你做下面的操作，那么do_something()将不会被调用：

1
2
3
unsigned short a=1;
a=a-5;
if (a < 0) do_something();

整数提升发生在(a-5)这里，但结果的整数值-4会被赋值到unsigned short的a里面。正如你所知道的，一个int型被转换为unsigned short会导致截断，最后导致a的值为一个非常大的正数。因此，比较表达式将不返回真。

规则3：整数提升后为相同类型

如果两个操作数在整数提升后是相同类型，那么久不必进行后面的类型转换，因为算术运算会被直接带到机器级别。这可能会在两边操作数都被提升到int型时发生，或者它们本身就是相同的没有被整数提升影响到的类型。

规则4：相同符号，不同类型

如果两个操作数在整数提升后是不同的类型，但是它们是否有符号位是相同的，那么窄的类型会被转换为宽的类型。换句话说，如果两边操作数都是signed或者两边都是unsigned，那么在整数转换层级上较低的类型会被转换成转换层级上较高的类型。

注意这个规则对于short或者符号类型没有用，因为它们早就通过整数提升变成了int。这个规则对于更大大小数的算术运算更管用，例如long long int或者long int。下面是一个例子：

1
2
3
4
int jim =5;
long int bob = 6;
long long int fred;
fred = (jim + bob);

整数提升不会改变任何类型，因为它们都是在宽度上大于或者等于int型的。因此这个规则会在加法开始前让jim被转换为long int，加法结果的类型是long int，然后再被转换为long long int赋值给fred。

在下一节中，你将会考虑操作数为不同类型，并且一个是signed另一个是unsigned。这种情况在安全层面上会有很多有趣的东西。

规则5：带符号类型比带无符号类型更宽

对于这个规则(signed遇见unsigned —by译者)，第一种情形就是unsigned操作数在转换等级上大于signed操作数，或者它们的等级是相同的的情况下，你将一个signed操作数转换为unsigned操作数。这个行为可能会震惊到你，然后导致像下面的情况：

1
2
3
int jim = -5;
if (jim < sizeof (int))
	do_something();

比较算符<会导致常规类型转换应用到两边的操作数。因此整数提升会应用到jim和sizeof(int)里，但这并不会影响到它们。然后继续进行常规算术转换，它试图照除哪个类型应该被当作比较的通用类型。在这种情况下，jim是带符号整数，sizeof(int)是size_t，也就是无符号整数类型。由于size_t在类型转换等级上更高，因此无符号类型在这里就有了优先级，因此，jim会被转换为无符号整数类型，然后比较表达式结果为假，do_something()不会被调用。在32位系统里，真实的比较是下面这样：

1
2
if (4294967291 < 4)
	do_something();
规则6：带符号类型比无符号类型更窄，能保值

如果带符号类型比无符号类型的转换等级更高，并且能够在从无符号类型到带符号类型执行保值转换，那么就会将任何东西转换为带符号整数。就如下面的例子：

1
2
3
long long int a=10;
unsigned int b= 5;
(a+b);

带符号变量为long long int，能够表示任何unsigned int的值，因此编译器会将两边操作数转换为带符号类型：long long int.

规则7：带符号类型比无符号类型更窄，不能保值

还有一项规则：如果带符号类型比无符号类型的转换等级更高，但是不是所有的无符号整数能表示的数带符号类型都能表示，那么就会发生有点奇怪的事。 获取带符号整数的类型，将其转换为对应的无符号整数类型，然后将两个操作数转换为该类型并使用。 下面是一个例子：

1
2
3
unsigned int a = 10;
long int b=20;
(a+b);

这个例子要假设在这个机器上，int类型和long int类型长度相同。假发算符会导致常规算术转换被应用。首先进行整数提升，但不会改变任何类型。带符号类型long int转换层级比无符号类型unsigned int更高。但带符号类型无法表示无符号类型的所有值。因此会启动最后这条规则。首先找到带符号操作数类型(long int)，对应相应的无符号类型，unsigned long int，然后将两边操作数都转换为unsigned long int。因此表达式结果类型为unsigned long int，值为30.

算术转换总结

下面是对有用的算术转换做总结。后面的表格也是同样的总结。

  • 如果任意一方是浮点数，双方操作数都会被转换为两边中精度最高的浮点数。这个你掌握了。
  • 对两边都进行整数提升。如果这两个操作数现在是相同类型的。这个你掌握了
  • 如果两个操作数在是否带符号，这种情况一样的会将低转换等级的一方转换为高转换等级的一方。这个你掌握了。
  • 如果无符号操作数等级大于等于带符号操作数，就将带符号操作数转换为无符号数。这个你掌握了。
  • 如果如果带符号操作数等级大于无符号操作数，并且能够进行保值转换，将无符号数转换为带符号数类型。这个你掌握了。
  • 如果如果带符号操作数等级大于无符号操作数，并且不能够进行保值转换，那就将两边都转换为带符号类型对应的无符号类型。
左操作数类型 右操作数类型 结果 公共类型
int float 左操作数转换为float float
double char 右操作数转换为double double
unsigned int int 右操作数转换为unsigned int unsigned int
unsigned short int 左操作数转换为int int
unsigned char unsigned short 左右两边操作数都转换为int int
unsigned int: 32 short 左右操作数都转换为int int
unsigned int long int 左右边操作数转换为unsigned long int unsigned long int
unsigned int long long int 左操作数转换为long long int long long int
unsigned int unsigned long long int 左操作数转换为unsigned long long int unsigned long long int
常规算术转换应用

现在你理解了常规算术转换，那就可以来看看这些转换被用在了哪里：

加法

加法可以在两个算术类型，以及算术类型和指针类型之间发生。指针运算会在小节“指针运算”中介绍。但现在，我们只需要考虑变量为算术类型，编译器会对两边使用常规算术转换。

减法

减法可以在两个算术类型，以及算术类型和指针类型之间发生。在两个算术类型进行减法的情况时，编译器会对两边使用常规算术转换。

乘法算符

算符* /的操作数两边都必须时算术类型，并且%的变量必须时整数类型。常规算术转换会被用到两边的操作数中。

关系和等价算符

当两个算术操作数被比较时，常规算术转换会被用到两边的操作数中。结果类似会是int，值为1或者0，取决于测试的结果。

二进制位级算符

二进制位级算符& ^ ！要求整数型操作数。常规算术转换会被使用。

问号标记算符(question mark operator)

从类型转换的视角看，条件运算符是C语言最有趣的算符之一。下面有一个例子可以看出它的应用有多广泛：

1
2
3
4
5
int a=1;
unsigned int b=2;
int choice=-1;
...
result = choice ? a : b ;

在这个例子中，第一个操作数choice如果为真，那么表达式的结果就是第二个操作数，也就是a，否则就是第三个操作数b。

编译器必须在编译时知道条件表达式的结果类型，这在这种情况下可能比较棘手。C语言所做的是确定对第二个和第三个参数运行常规算术转换后的结果是哪种类型，并使该类型成为表达式的结果类型。因此，在前面的示例中，无论choice的值是什么，表达式的结果都是unsigned int。

类型转换总结

下面的表格总结了一些常见类型转换的细节：

操作 操作数类型 类型转换 结果类型
强制类型转换 (type) expression 表达式通过简单转换被转换为type type
赋值= 右边操作数通过简单转换转换为左边操作数类型 左边操作数类型
带有原型的函数调用 使用简单转换转换变量，转换取决于原型 函数的返回类型
不带有原型的函数调用 变量通过常规变量提升，即整数提升 int
一元算符返回+,- +a -a 操作数类型必须为算术类型 操作数通过整数提升 操作数提升后的类型
一元算符~ ~a 操作数类型必须为整数类型 操作数通过整数提升 操作数提升后的类型
位级算符<<和>> 操作数类型必须为整数类型 操作数通过整数提升 左边操作数提升后的类型
switch语句 表达式必须为整数类型 表达式通过整数提升，case会被转换为这个类型
二元算符+ - 操作数类型必须为算术类型或者*pointer(在指针运算中有介绍) 操作数通过常用算术转换 常用算术转换的公共类型
二元算符* \ 操作数类型必须为算术类型 操作数通过常用算术转换 常用算术转换的公共类型
二元算符 % 操作数类型必须为整数类型 操作数通过常用算术转换 常用算术转换的公共类型
二元下标[] a[b] 解释为*((a)+(b))
二元算符! 操作数类型必须为算术类型或者指针 int,值为0或者1
sizeof size_t(无符号整数类型)
二元算符> < <= >= == != 操作数类型必须为算术类型或者*pointer(在指针运算中有介绍) 操作数通过常用算术转换 常用算术转换的公共类型
二元算符& ^ | 操作数类型必须为整数类型 操作数通过常用算术转换 常用算术转换的公共类型
二元算符&& | | 操作数类型必须为算术类型或者指针 int，值为0或1
条件三元算符? 第二或者第三操作数必须为算术类型或者指针 第二第三操作数通过常用算术转换 常用算术转换的公共类型
审计提示：类型转换

即使那些广泛研究过转换的人也会对编译器将某些表达式呈现为汇编的方式感到惊讶。当你看到让你觉得可疑或可能含糊不清的代码时，请毫不犹豫地编写一个简单的测试程序或研究生成的程序集，以验证你的直觉。

如果你生成程序集来验证或研究本章中讨论的转换，请注意C编译器可以优化某些转换，或使用架构技巧，这可能会使程序集看起来不正确或不一致。在概念层面上，编译器的行为与C标准描述的一样，并且它们最终生成遵循规则的代码。但是，由于优化，程序集可能看起来不一致，甚至不正确，因为它可能操作寄存器中不应该使用的部分。

7.2.6 类型转换漏洞

现在你对C语言类型转换有了坚实基础了，现在来探寻一些它们能够创造的异常情况。 隐式类型转换在某些情况下会让程序员猝不及防。本小节会主要集中在带符号和无符号数的简单转换，符号位扩展，截断，以及常见算术转换， 专注于比较。

带符号/无符号转换

大多数和类型转换相关的安全问题都是由带符号和无符号数之间的简单转换造成的。这里我们只探讨赋值，函数调用，强制类型转换的情形。

快速复习一下简单转换规则，当带符号数转换为相同大小的无符号数时，位模式被保留，然后值也会相应变化。当无符号数转换为带符号数时也会发生相同的事。严格来说，无符号到带符号数的转换是实现定义的，但在二进制补码是线下，通常位模式被保留。

这种转换最重要的情况是在函数调用期间，如本例所示 ：

1
2
3
4
5
int copy(char *dst, char *src, unsigned int len)
{
    while (len--)
    *dst++ = *src++;
}

第三个参数是一个unsigned int，用来表示内存中需要复制的长度。如果你将一个signed int传入这个函数当作第三个参数，那么它将会被转换为无符号整数，假如你这么做：

1
2
int f = -1;
copy(mydst, mysrc, f);

copy()函数将会看到一个非常大的len并且极有可能执行复制直到产生分段错误(segmentation fault)。几乎所有的libc例行程序都将大小参数的类型定为size_t，这是一种和指针长度相等的无符号类型。这也是为什么你必须永远不要将一个负长度的参数被传入libc例行程序重，例如snprintf(), strncpy(), memcpy(), read(), 或者strncat() 。

这种情况经常发生，特别是带符号整数被用作长度值并且程序员并没有考虑可能小于0的情况。在这种场合，所有小于0的值在被强制转换为无符号类型时都会被改为很大的正数。不怀好意的用户经常会将特定的负整数传入很多程序接口中然后破坏程序逻辑。这种类型的bug在用户指定的整数上的最大长度检查时经常发生， 但是没有检查该整数是否为负，就像下面的代码所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int read_user_data(int sockfd)
{
	int length, sockfd, n;
	char buffer[1024];
	length = get_user_length(sockfd);
	if(length > 1024){
		error("illegal input, not enough room in buffer\n");
	return 1;
	}
	if(read(sockfd, buffer, length) < 0){
		error("read: %m");
		return 1;
	}
	return 0;
}

在上面的代码中，假设get_user_length()函数从网络中读取一个32位整数。如果用户提供的长度为负数，则可以避免长度检查，从而危及应用程序。对于read()调用，一个负长度被转换为size_t类型，正如你所知道的，它将转换为一个大的无符号值。代码审查人员应该始终考虑带符号类型中的负值的含义，并查看是否会产生可能导致安全性暴露的意外结果。在这种情况下，由于错误的长度检查，可能触发缓冲区溢出;因此，这个疏忽是相当严重的。

审计技巧：带符号/无符号转换

你希望查找这样的情况:函数采用size_t或无符号整型长度参数，而程序员传递一个可能会受到用户的影响的有符号整数。适合查找的函数包括read()、recvfrom()、memcpy()、memset()、bcopy()、snprintf()、strncat()、strncpy()和malloc()。如果用户可以强制程序传入一个负值，那么函数将其解释为一个大值，这可能导致一个可利用的条件。

另外，查找直接从网络读取的长度参数位置，或者用户通过某种输入机制指定的位置。如果在代码的某些部分中将长度解释为带符号的变量，则应该评估用户提供负值的影响。

在检查应用程序中的函数时，最好在函数审计日志中注意每个函数的参数的数据类型。这样，每次审计对该函数的后续调用时，就可以简单地比较类型并对照本章中的转换表，来准确预测将会发生什么，以及这种转变的含义。 在第7章“程序构建模块”中，你会学到更多关于分析函数以及保持函数原型和行为的日志。

符号位扩展

符号位扩展发生在将带符号的较小整数类型转换为较大类型时，并且机器通过较大类型的未使用位传播较小类型的符号位。符号位扩展的目的是在从较小的有符号类型转换为较大的有符号类型时保值。

如你所知，符号位扩展可以以多种方式出现。首先，如果通过类型转换、赋值或函数调用从小带符号类型到大带符号类型进行简单转换，则会发生符号位扩展。你还知道，如果通过整数提升提升了小于整数的有符号类型，则会发生符号位扩展。符号位扩展还可能是在整型提升之后应用常规算术转换的结果，因为有符号整数类型可以升级为更大的类型，比如long long。

符号位扩展是该语言的一个自然组成部分，它对于整数的值保持提升是必要的。那么，为什么提到它是一个安全问题呢?有两个原因 ：

  • 在某些情况下，符号位扩展是会产生意外结果的变值转换。
  • 程序员总是忘记他们使用的char和short类型是有符号的!

要检查第一个原因，如果你还记得转换部分，一个更有趣的发现是，如果将较小的有符号类型转换为较大的无符号类型，则会执行符号位扩展。假设一个程序员做了这样的事情：

1
2
3
char len;
len=get_len_field();
snprintf(dst, len, "%s", src);

这段代码写得一团糟。如果get_len_field()的结果使得len的值小于0，那么这个负值将作为长度参数传递给snprintf()。假设程序员试图修复此错误并执行以下操作：

1
2
3
char len;
len=get_len_field();
snprintf(dst, (unsigned int)len, "%s", src);

这个解决方案有点道理。一个无符号整数不可能是负的，对吧?不幸的是，符号位扩展发生在从char到unsigned int的转换过程中，因此试图删除小于0的字符会适得其反。如果len恰好小于0，(unsigned int)len就会得到一个大的值。

这个示例看起来有些随意，但是它类似于作者最近在客户机代码中发现的一个实际bug。这个故事的寓意是，你应该始终记住，在从较小的有符号类型转换为较大的无符号类型时，将应用符号位扩展。

第二个原因是程序员总是忘记他们使用的char和short类型是有符号的。这句话听起来非常正确，特别是在处理带符号整数长度的网络代码或每次处理一个字符的二进制或文本数据的代码中。看看l0pht的反嗅探(antisniff)工具( http://packetstormsecurity.org/sniffers/antisniff/ ) 的DNS包解析代码中一个真实存在的漏洞。它是演示前面讨论过的一些漏洞的绝佳错误。首先在该软件中发现了涉及不当使用strncat()的缓冲区溢出，在该漏洞被修补后，TESO的研究人员发现，由于符号位扩展问题，该软件仍然很脆弱。由于对符号位扩展问题的修复不正确，他们又发布了另一个漏洞。下面的示例将带你了解此漏洞的时间轴。

下面的代码在raw_watchdn .c文件的watch_dns_ptr()函数中包含了反嗅探研究发布版本1中稍微编辑过的易受攻击的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
char *indx;
int count;
char nameStr[MAX_LEN]; //256
...
memset(nameStr, '\0', sizeof(nameStr));
...
indx = (char *)(pkt + rr_offset);
count = (char)*indx;
while (count){
	(char *)indx++;
	strncat(nameStr, (char *)indx, count);
	indx += count;
	count = (char)*indx;
	strncat(nameStr, ".",
	sizeof(nameStr) strlen(nameStr));
}
nameStr[strlen(nameStr)-1] = '\0';

在理解这段代码之前，需要了解一些背景知识。watch_dns_ptr()函数的目的是从包中提取域名，并将其复制到nameStr字符串中。DNS包中的DNS域名有点像Pascal字符串。域名中的每个标签都有一个包含其长度的字节作为前缀。当你到达一个大小为0的标签时，域名结束。(DNS压缩方案与此漏洞无关。)图6-8显示了DNS域名在包中的样子。有三个标签 test、jim和com，以及一个0长度的标签，用于指定名称的结束。

6-8

该代码首先从包中读取第一个长度字节，并将其存储为整数count。这个长度字节是存储在整数中的带符号字符，因此你应该能够在count中放入-128到127之间的任何值。记住这一点，后面会用到。

while()循环继续读取标签，并在标签上调用strncat()到nameStr字符串。发布的第一个漏洞是在这个循环中没有长度检查。如果你只是在包中提供一个足够长的域名，那么它可能写过nameStr[]的边界。下面的代码显示了研究版本1.1中如何修复这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
char *indx;
int count;
char nameStr[MAX_LEN]; //256
...
memset(nameStr, '\0', sizeof(nameStr));
...
indx = (char *)(pkt + rr_offset);
count = (char)*indx;
while (count){
	if (strlen(nameStr) + count < ( MAX_LEN - 1) ){ //这一行加粗
	(char *)indx++;
	strncat(nameStr, (char *)indx, count);
	indx += count;
	count = (char)*indx;
	strncat(nameStr, ".",
	sizeof(nameStr) strlen(nameStr));
} else { //这一行加粗
	fprintf(stderr, "Alert! Someone is attempting " 
					"to send LONG DNS packets\n");
	count = 0;
	} // else括号里的都加粗
}
nameStr[strlen(nameStr)-1] = '\0';

代码基本相同，但是增加了长度检查，以防止缓冲区溢出。在循环的顶部，程序在执行字符串连接之前检查以确保缓冲区中有足够的空间用于count字节。现在在考虑符号位扩展漏洞的情况下检查这段代码。计数可以是-128到127之间的任意值，如果计数为负数会怎样呢?看看长度检查部分：

1
if (strlen(nameStr) + count < ( MAX_LEN - 1) ){

你知道，strlen(nameStr)会返回一个size_t，在32位系统中也就是等同于unsigned int，你同样直到，count是一个小于0的数，假如这个循环已经进行了一次，并且strlen(nameStr)是5，并且count是-1，对于加法，count会被转换为无符号整数，也就是(5+4,294,967,295)，这将造成算术溢出然后得到一个小的值，例如4，4小于(MAX_LEN-1)，也就是256，这看起来还是很好的。接下来，你会看到count（值被你设为-1）被传入strcat()里，strcat()函数取的是size_t，因此这个值会被解释为4,294,967,295。因此，你又取得了漏洞利用的胜利。你可以将足够多的你想要的信息写入nameStr字符串中。

下面的代码显示了这个漏洞在研究发布版本1.1.1中是如何被解决的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
char *indx;
int count;
char nameStr[MAX_LEN]; //256
...
memset(nameStr, '\0', sizeof(nameStr));
...
indx = (char *)(pkt + rr_offset);
count = (char)*indx;
while (count){
    /* typecast the strlen so we aren't dependent on
    the call to be properly setting to unsigned. */
    if ((unsigned int)strlen(nameStr) +
        (unsigned int)count < ( MAX_LEN - 1) ){
        //上面两行加粗
        (char *)indx++;
        strncat(nameStr, (char *)indx, count);
        indx += count;
        count = (char)*indx;
        strncat(nameStr, ".",
        sizeof(nameStr) strlen(nameStr));
    } else {
        fprintf(stderr, "Alert! Someone is attempting "
        "to send LONG DNS packets\n");
        count = 0;
    }
}
nameStr[strlen(nameStr)-1] = '\0';

这个解决方案基本上就是相同的代码，除了强制类型转换被加入了长度检查中。在下面的代码体现：

1
2
if ((unsigned int)strlen(nameStr) +
	(unsigned int)count < ( MAX_LEN - 1) ){

strlen()的结果会被强制转换为unsigned int，显然是多余的举动，因为它已经是size_t了。count会被强制类型转换为unsigned int。这也是多余的，因为它会被加法运算符隐式地转换为无符号整数类型。本质上来说，什么都没有改变。你仍然可以将一个负值标签长度传入然后通过长度检查！下面的代码显示了这个问题是如何在1.1.2版本中解决的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
unsigned char *indx;
unsigned int count;
unsigned char nameStr[MAX_LEN]; //256
//上面三行加粗
...
memset(nameStr, '\0', sizeof(nameStr));
...
indx = (char *)(pkt + rr_offset);
count = (char)*indx;
while (count){
    if (strlen(nameStr) + count < ( MAX_LEN - 1) ){
        indx++;
        strncat(nameStr, indx, count);
        indx += count;
        count = *indx;
        strncat(nameStr, ".",
        sizeof(nameStr) strlen(nameStr));
    } else {
        fprintf(stderr, "Alert! Someone is attempting "
        "to send LONG DNS packets\n");
        count = 0;
    }
}
nameStr[strlen(nameStr)-1] = '\0';

开发者将count,nameStr，indx变为了无符号数然后回到了以前版本的长度检查。因此，你现在使用的符号位扩展似乎消失了，因为字符指针indx现在是无符号类型。但是，仔细看看这一行:

1
count = (char)*indx;

这份代码解引用了indx，它是一个unsigned char指针。这会给你一个无符号的字符，它会被显式地转换为signed char。你知道在位模式上不会改变， 这样就回到了-128到127的范围。它被赋值给无符号整型，但是你知道从较小的有符号类型转换为较大的无符号类型会导致符号位扩展。因此，由于类型转换到(char)，你仍然可以在循环中获得一个恶意的大count，但仅针对第一个标签。现在看看这个长度检查：

1
if (strlen(nameStr) + count < ( MAX_LEN - 1) ){

不幸地是，strlen(nameStr)在第一次循环时是0，因此任意大值的count不会比(MAX_LEN-1)小， 然后你被抓住，被踢出了循环。接近了，但还不清楚。有趣的是，如果你在第一次进入循环时被踢出，程序将执行以下操作：

1
nameStr[strlen(nameStr)-1] = '\0';

由于strlen(nameStr)是0，意思就是它在缓冲区后面1字节处写入0，在nameStr[-1]。 现在你已经从20-20的后见之明的角度了解了修复的发展，请看下面的代码，这是一个基于short整数数据类型的示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
unsigned short read_length(int sockfd)
{
    unsigned short len;
    if(full_read(sockfd, (void *)&len, 2) != 2)
        die("could not read length!\n");
        return ntohs(len);
    }
    int read_packet(int sockfd)
    {
        struct header hdr;
        short length;
        char *buffer;
        length = read_length(sockfd);
        if(length > 1024){
        error("read_packet: length too large: %d\n", length);
        return 1;
    }
    buffer = (char *)malloc(length+1);
    if((n = read(sockfd, buffer, length) < 0){
        error("read: %m");
        free(buffer);
        return 1;
    }
    buffer[n] = '\0';
    return 0;
}

许多在本章中探索过的概念都会在这里起作用。首先，read_length()函数的结果是unsigned short int，会被转换为signed short int然后被储存在length中。在接下来的长度检查中，比较的两边都会被提升为整数。如果length是一个负数，只要它大于1024就会通过检查。接下来的一行将length加一然后传入malloc()的第一个参数。length参数再一次符号位扩展因为它会被加法提升为整数。因此，如果length的值设为0xFFFF，符号位扩展后就是0xFFFFFFF。这个值加1会环绕到0，然后malloc(0)返回一个非常小的内存。最终，read()的效用造成第三个变量，length参数被直接从short int转换为size_t。符号位扩展会发生因此这是一个小的带符号类型转换为大的无符号类型的情况。因此对read()的调用允许你从缓冲区中读入非常大数目的字节，造成潜在的缓冲区溢出。

另一个典型的例子是程序员在使用ctype libc函数时忘记小类型是否有符号。考虑toupper()函数，它具有以下原型：

1
int toupper(int c);

toupper()函数在绝大多数libc实现中通过在查找表中搜索正确答案来工作。 一些libc不能正确地处理负数参数，和在内存中对表进行的索引。 下面toupper()的定义不常见：

1
2
3
4
int toupper(int c)
{
    return _toupper_tab[c];
}

现在假如你做像下面的事情：

1
2
3
4
5
6
7
8
void upperize(char *str)
{
    while (*str)
    {
        *str = toupper(*str);
        str++;
    }
}

如果libc实现没有健壮的toupper()函数，则可能会对字符串进行一些奇怪的更改。如果其中一个字符是-1，那么它将被转换为一个值为-1的整数，toupper()函数将在其内存中的表后面进行索引。

看看程序员不考虑符号位扩展的最后一个实际例子。下面是是安全研究员Michael Zalewski发现的一个Sendmail漏洞(www.cert.org/advisories/CA-2003-12.html)。它来自Sendmail版本8.12.3中的prescan()函数，主要负责将电子邮件地址解析为令牌(来自sendmail /parseaddr.c)。为简洁起见，这里对代码进行了编辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
register char *p;
register char *q;
register int c;
...
p = addr;
for (;;)
{
	/* store away any old lookahead character */
	if (c != NOCHAR && !bslashmode)
	{
		/* see if there is room */
		if (q >= &pvpbuf[pvpbsize - 5])
		{
			usrerr("553 5.1.1 Address too long");
			if (strlen(addr) > MAXNAME)
				addr[MAXNAME] = '\0';
returnnull:
            if (delimptr != NULL)
                *delimptr = p;
            CurEnv->e_to = saveto;
            return NULL;
		}
		/* squirrel it away */
		*q++ = c;
	}
	/* read a new input character */
	c = *p++;
    
	..

	/* chew up special characters */
	*q = '\0';
	if (bslashmode)
	{
		bslashmode = false;
		/* kludge \! for naive users */
		if (cmntcnt > 0)
		{
			c = NOCHAR;
			continue;
		}
		else if (c != '!' || state == QST)
		{
			*q++ = '\\';
			continue;
		}
	}
	if (c == '\\')
	bslashmode = true;
}

NOCHAR常数定义为-1， 用于表示处理字符时的某些错误条件。变量p处理一个用户提供的地址，并在读取完整的符号(token)后退出循环。在循环中有一个长度检查;但是，只有当两个条件为真时才检查它:当c不是NOCHAR(即，c != -1)和bslashmode为假时。问题在这一行:

1
c = *p++;

由于p指向的字符的符号位扩展，用户可以指定字符0xFF并将其扩展到0xFFFFFFFF，也就是NOCHAR。如果用户提供一个重复模式，即0x2F(反斜杠字符)后跟0xFF，则循环可以连续运行，而不需要在顶部执行长度检查。这将导致反斜杠连续写入目标缓冲区，而不检查是否还有足够的空间。因此，由于存储在变量c中的字符被标记扩展，会触发一个意外的代码路径，从而导致缓冲区溢出。

这一漏洞还加强了本章开头所述的另一项原则。编译器执行的隐式操作很微妙，在检查源代码时，你需要检查类型转换的含义，并预期程序将如何处理意外值(在本例中是NOCHAR值，由于符号位扩展，用户可以指定它)。

符号位扩展似乎应该是普遍存在的，而且在C代码中基本无害。但是，程序员在转换较小的数据类型时很少打算使用符号位扩展，符号位扩展的出现通常表明存在错误。符号位扩展在C中很难定位，但是它在汇编代码中很好地表现为movsx指令。尝试通过汇编练习搜索符号位扩展转换，然后将它们与源代码关联起来，这是一种有用的技术。

1
2
3
4
5
6
7
8
//符号位扩展示例
unsigned int l;
char c=5;
l=
//零扩展示例
unsigned int l;
unsigned char c=5;
l=

假设实现调用有符号字符，你知道符号位扩展将出现在上面符号位扩展示例中，而不是零扩展示例。比较生成的汇编代码，如下表所示。

符号位扩展 零扩展
mov [ebp+var_5], 5 mov [ebp+var_5], 5
movsx eax, [ebp+var_5] xor eax, eax
mov al, [ebp+var_5]
mov [ebp+var_4], eax mov [ebp+var_4], eax

可以看到，在符号位扩展示例中，使用了movsx指令。在零扩展示例中，编译器首先使用xor eax、eax清除寄存器，然后将字符字节移动到该寄存器中。

审计提示:符号位扩展

在寻找与符号位扩展相关的漏洞时，你应该关注处理带符号字符值/指针或有符号短整数值/指针的代码。通常，你可以在字符串处理代码和对带有长度元素的数据包进行解码的网络代码中找到它们。通常，你希望查找具有字符或short整数类型的代码，并在将其转换为整数的上下文中使用它。记住，如果看到带符号字符或signed short转换为无符号整数，仍然会出现符号位扩展。 如前所述，查找符号位扩展漏洞的一种有效方法是搜索movsx指令的应用程序二进制代码的汇编代码。在搜索代码中可能存在漏洞的位置时，这种技术通常可以帮助你穿越typedef、宏和类型转换的多个层面的干扰。

截断

截断(truncation)经常在大类型转换为小类型时发生。请注意常规算术转换以及整数提升实际上从未要求将大型类型转换为较小的类型。因此，截断只能在赋值、类型转换或涉及原型的函数调用时发生。这里有一个截断的简单例子：

1
2
3
int g = 0x12345678;
short int h;
h = g;

当g赋值到h时，前16字节的值就会被截断，h的值会变成0x5678。因此如果这种数据丢失的情况如果程序员并没有预期到的话，就肯定会造成安全问题。下面的代码基于历史版本的网络文件系统(Network File System, NFS)的整数截断安全漏洞：

1
2
3
4
5
6
7
8
9
10
11
void assume_privs(unsigned short uid)
{
    seteuid(uid);
    setuid(uid);
}
int become_user(int uid)
{
    if (uid == 0)
	    die("root isnt allowed");
    assume_privs(uid);
}

公平地说，这个漏洞大多是趣闻轶事，它的存在并没有通过源代码验证。NFS禁止用户使用root权限远程装载磁盘。最终，攻击者发现他们可以指定一个UID为65536，它将通过防止root访问的安全检查。但是，这个UID将被分配给一个unsigned short整数类型，并被截断为一个值0。因此，攻击者可以假定root用户的UID为0，从而绕过保护。

在查看真实的截断问题之前，请先查看下面代码中的另一个合成漏洞：

1
2
3
4
5
6
7
8
unsigned short int f;
char mybuf[1024];
char *userstr=getuserstr();

f=strlen(userstr);
if (f > sizeof(mybuf)-5)
	die("string too long!");
strcpy(mybuf, userstr);

strlen()函数的返回值是size_t，被转换成了unsigned short。如果一个字符串有66,000个长度的字符，那么截断就会发生，f的值将会是464.因此，对函数strcpy()的长度检查保护就会被突破，缓冲区溢出就会发生。

大多数SSH守护进程中的一个停止显示(show-stopping)的错误是由整数截断引起的。具有讽刺意味的是，易受攻击的代码是在一个旨在解决另一个安全漏洞的函数中，即由CORE-SDI识别的SSH插入攻击。关于这次攻击的详细信息可以在 www1.corest.com/files/files/11/CRC32.pdf. 上找到。

这种攻击的本质是，攻击者可以对块密码使用一种已知的聪明的明文攻击，将他们选择的少量数据插入到SSH流中。通常，这种攻击可以通过消息完整性检查来阻止，但是SSH使用了CRC32, CORE-SDI的研究人员找到了在SSH协议上下文中规避它的方法。

包含截断漏洞的函数的职责是确定插入攻击是否发生。这些插入攻击的一个属性是在包的末尾有一长串类似的字节，目的是操纵CRC32值，使其正确。设计的防御措施是搜索数据包中的重复块，然后进行CRC32计算直到重复点，以确定是否发生了任何操作。这种方法对于小数据包来说很容易，但是对于大数据集可能会产生性能影响。因此，大概是为了解决性能影响，我们使用了一种哈希方案。

你将要看到的函数有两个独立的代码路径。如果数据包小于一定的大小，它就对数据进行直接分析。如果大于这个大小，则使用哈希表来提高分析效率。没有必要了解功能来理解脆弱性。但是，如果你感到好奇，你将看到用于较小数据包的更简单的情况，其算法大致如下面代码所示。

1
2
3
4
5
6
7
8
9
10
11
for c = 包中的每8位块
	if c 等于初始化向量块
		检查c是否遭受攻击.
		如果检查成功, 返回DETECTED.
		如果检查失败, 则没有遭受攻击，返回OK.
	for d = c之前包中的每8位块
		如果d等于c, 检查c是否遭受攻击.
			如果检查成功, 返回DETECTED.
			如果检查失败, break出d的循环.
	next d
next c

该代码遍历包中的每个8字节块，如果它看到包中与当前块相同的块，它就检查是否正在进行攻击.

代码中基于哈希表的路径稍微复杂一些。它们的算法广义上是相同的，但不是比较一堆8字节的块，而是对每个块的32位的哈希值来进行比较。哈希表由8字节块的32位哈希索引，对哈希表的大小取模，而bucket包含最后哈希到该bucket的块的位置。在哈希表的构造和管理中存在截断问题。下面代码包含代码的开头部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* Detect a crc32 compensation attack on a packet */
int
detect_attack(unsigned char *buf, u_int32_t len,
			unsigned char *IV)
{
	static u_int16_t *h = (u_int16_t *) NULL;
	static u_int16_t n = HASH_MINSIZE / HASH_ENTRYSIZE;
	register u_int32_t i, j;
	u_int32_t l;
	register unsigned char *c;
	unsigned char *d;
	if (len > (SSH_MAXBLOCKS * SSH_BLOCKSIZE) ||
		len % SSH_BLOCKSIZE != 0) {
		fatal("detect_attack: bad length %d", len);
	}

首先，这份代码检查了包是否足够长或者是否不是8字节的倍数。SSH_MAXBLOCKS是32,768，BLOCKSIZE是8，因此包的大小能够达到262,144字节。在下面的代码，n从HASH_MINSIZE / HASH_ENTRYSIZE开始，也就是8,192/2=4096，目的是保存哈希表中的入口数：

1
2
for (l = n; l < HASH_FACTOR(len / SSH_BLOCKSIZE); l = l << 2)
	;

哈希表初始大小是8,192个元素。这个循环尝试得到一个对于哈希表较好的大小。它先从一个n的猜测值开始，也就是当前大小，然后检查它是否对于包足够大，如果不是，那就通过左移两次将l增大四倍。因为包中有8字节的块，它通过确定对于8位块是否有对应2/3数目的哈希表入口决定哈希表是否足够大。HASH_FACTOR定义为((x)*3/2)。下面的代码就是有趣的部分了：

1
2
3
4
5
6
7
8
9
10
11
if (h == NULL) {
	debug("Installing crc compensation "
		"attack detector.");
	n = l;
	h = (u_int16_t *) xmalloc(n * HASH_ENTRYSIZE);
} else {
	if (l > n) {
		n = l;
		h = (u_int16_t *)xrealloc(h, n * HASH_ENTRYSIZE);
	}
}

如果h为NULL，就表示这是第一次通过这个函数，你需要为新的哈希表分配空间。如果你记得的话，l是计算后得到的哈希表大小，n包含了哈希表入口数量。如果h不为NULL，就表明哈希表已经分配过了。然而，如果当前哈希表对于新的计算过的l并没有足够大，然后就回到前面重新分配。

你已经看过足够的代码了，现在可以看它的问题了：n是unsigend short int。如果你传入的包大小够大，l，一个unsigned int，就可能得到一个大于65,535的值，当l传入n时，截断就会发生。例如，假如你传入一个大小为262,144字节大小的包。首先它通过了第一个检查，然后在循环中，l会像下面这样改变：

1
2
3
Iteration 1: l = 4096 l < 49152 l<<=4
Iteration 2: l = 16384 l < 49152 l<<=4
Iteration 3: l = 65536 l >= 49152

当l的值为65,536，被传入n时，前面16位就会截断，然后n的值就会是0.在现代操作系统中，malloc(0)的结果是一个指向小对象的合法返回指针，然后函数后面的行为就非常可疑。

在接下来函数的部分中，这些代码进行直接分析，由于他们并没有直接使用哈希表，因此并不那么有趣：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
if (len <= HASH_MINBLOCKS) {
	for (c = buf; c < buf + len; c += SSH_BLOCKSIZE) {
		if (IV && (!CMP(c, IV))) {
			if ((check_crc(c, buf, len, IV)))
				return (DEATTACK_DETECTED);
			else
				break;
			}
			for (d = buf; d < c; d += SSH_BLOCKSIZE) {
				if (!CMP(c, d)) {
					if ((check_crc(c, buf, len, IV)))
						return (DEATTACK_DETECTED);
					else
						break;
					}
				}
			}
	return (DEATTACK_OK);
}

接下来是执行基于哈希的检测例程的代码。在下面的代码中，请记住n的值是0，h是一个在堆中很小但合法的对象。在这种情况下，就可以在进程内存中做一些有趣的事：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
memset(h, HASH_UNUSEDCHAR, n * HASH_ENTRYSIZE);
if (IV)
	h[HASH(IV) & (n - 1)] = HASH_IV;
for (c = buf, j = 0; c < (buf + len); c += SSH_BLOCKSIZE, j++) {
	for (i = HASH(c) & (n - 1); h[i] != HASH_UNUSED;
		i = (i + 1) & (n - 1)) {
		if (h[i] == HASH_IV) {
			if (!CMP(c, IV)) {
				if (check_crc(c, buf, len, IV))
					return (DEATTACK_DETECTED);
				else
					break;
				}
			} else if (!CMP(c, buf + h[i] * SSH_BLOCKSIZE)) {
				if (check_crc(c, buf, len, IV))
					return (DEATTACK_DETECTED);
				else
					break;
				}
			}
			h[i] = j;
		}
	return (DEATTACK_OK);
}

如果你没有立刻看出在这个循环中实施攻击的方法，不用担心。(你很好，代码还缺少一些关键的宏定义。)这个bug非常的微妙，对它的利用很复杂并且要动点脑子。事实上，这个漏洞对于很多角度来说是独一无二的。它强调了安全编程是非常困难的，每个人都会犯错，就算CORE-SDI这个世界上最有技术含量的安全公司。它仍然展现了有时候一个简单的黑盒测试仍然不能发现一些难以在源代码审计中发现的漏洞。这个漏洞的发现者，Micheal Zalewski， 以一种令人震惊的直接方式定位了这个弱点(ssh -l long_user_name).最终， 它强调了一个值得注意的例子，在这个例子中，编写一个漏洞比找到它的根漏洞更加困难。

译者注：

这个漏洞的描述是这样的(节选)：

By sending a crafted SSH1 packet to an affected host, an attacker can cause the SSH daemon to create a hash table with a size of zero. When the detection function then attempts to hash values into the null-sized hash table, these values can be used to modify the return address of the function call, thus causing the program to execute arbitrary code with the privileges of the SSH daemon, typically root.

翻译为中文就是：

通过向受影响的主机发送精心设计的SSH1包，攻击者可以导致SSH守护进程创建一个大小为0的哈希表。当检测函数尝试对空哈希表进行哈希索引时，这些值可以用来改变调用函数的返回地址，最终导致程序在使用SSH守护进程的权限(一般为root)下执行任意代码。

带有漏洞的守护进程源代码和漏洞描述见 https://web.archive.org/web/20051013074750/http://www.kb.cert.org/vuls/id/945216

审计提示：截断

当整数值被分配给较小的数据类型(如short整数类型或字符)时，通常会发现与截断相关的漏洞。要查找截断问题，请查找使用这些较短数据类型跟踪长度值或保存计算结果的位置。寻找潜在变量的一个好地方是在结构体定义中，特别是面向网络的代码。

程序员通常使用short或字符数据类型，只是因为变量的预期值范围很好地映射到该数据类型。但是，使用这些数据类型通常会导致未预期的截断。

比较

你已经看到了在长度检查中对负数进行符号比较的示例，以及它们如何暴露安全性问题。 另一个潜在的危险情况是比较具有不同类型的两个整数。如你所知，在进行比较时，编译器首先对操作数执行整数提升，然后对操作数执行常规的算术转换，以便可以对兼容类型进行比较。因为这些提升和转换可能会导致值的更改(因为符号的更改)，所以比较可能不会完全按照程序员的意图进行。攻击者可以利用这些转换来规避安全性检查，并经常危及应用程序。

为了看看比较可以怎样地走错路，可以参见下面的代码。这份的代码从网络中读取一个short整数，以确定读入包的长度。长度检查的前半段比较了(length-sizeof(short))和0来确保长度不会小于sizeof(short)。 如果是，那么在read()语句中稍后减去sizeof(short)时，它可以环绕成一个大整数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#define MAX_SIZE 1024
int read_packet(int sockfd)
{
	short length;
    char buf[MAX_SIZE];
	length = network_get_short(sockfd);
	if(length-sizeof(short) <= 0 || length > MAX_SIZE){
		error("bad length supplied\n");
		return 1;
	}
	if(read(sockfd, buf, length sizeof(short)) < 0){
		error("read: %m\n");
		return 1;
	}
	return 0;
}

第一个检查实际上是不正确的。注意sizeof运算符的返回类型是size_t，一个无符号类型。因此对于减法(length-sizeof(short))来说，length首先会被整数提升为signed int，然后被常规算术转换转换为无符号整数类型。减法运算的最终类型为无符号整数类型。最后，减法的结果永远不可能小于0，因此这个检查实际上什么都没有做。·为length提供一个值1可以避免if语句前半部分中的length检查在read()调用中试图防止并触发整数下溢的情况。

可以提供多个值以规避这两个检查并触发缓冲区溢出。如果length是一个负数，例如0xFFFF，那么第一个检查会通过，因为减法的结果类型是无符号的。第二个检查(length>MAX_SIZE)仍然会通过，因为length在比较时是一个signed int，并且是个负数，那么它就小于MAX_SIZE(1024)。 这个结果表明length变量在一种情况下是无符号的，而在另一种情况下是有符号的，因为在比较中使用了其他操作数。

在处理小于int的数据类型时，整型提升会使窄值变成带符号整数。这是一种保值的整数提升，本身并不是什么大问题。但是，有时候比较可能无意中被提升为有符号类型。下面的代码说明了这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int read_data(int sockfd)
{
    char buf[1024];
    unsigned short max = sizeof(buf);
    short length;
    length = get_network_short(sockfd);
    if(length > max){
        error("bad length: %d\n", length);
        return 1;
    }
    if(read(sockfd, buf, length) < 0){
        error("read: %m");
        return 1;
    }
	... process data ...
	return 0;
}

这份代码阐释了为什么你必须清楚在比较中你使用的类型结果是什么。max和length变量都是short整数类型，因此，它们会被提升为带符号整数。这意味着任何length提供的负值都会越过和max的长度检查。 由于在比较中执行数据类型转换，不仅可以避免完整性检查，而且会使整个比较变得无用，因为它检查的是不可能的条件。 考虑下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int get_int(char *data)
{
    unsigned int n = atoi(data);
    if(n < 0 || n > 1024)
        return 1;
        return n;
    }
    int main(int argc, char **argv)
    {
        unsigned long n;
        char buf[1024];
        if(argc < 2)
        exit(0);
        n = get_int(argv[1]);
        if(n < 0){
        fprintf(stderr, "illegal length specified\n");
        exit(-1);
    }
    memset(buf, 'A', n);
    return 0;
}

这份代码检查了变量n，以确保它落在0到1024的范围内。由于变量n是无符号的，小于0的检查就是不可能的。因为任何可以表示的值都必须为正数。潜在的漏洞非常微妙；如果攻击者在argv[1]中提供一个非法的整数，get_int()返回-1，然后在赋值给n后被转换成unsigned long。因此，这就会变为一个很大的值然后导致menset()让程序崩溃。

编译器可以检测永远不会为真的条件，并在传递某些标志时发出警告。看看用GCC编译前面的代码时会发生什么 ：

1
2
3
4
5
6
7
8
9
[root@doppelganger root]# gcc -Wall -o example example.c
[root@doppelganger root]# gcc -W -o example example.c
example.c: In function 'get_int':
example.c:10: warning: comparison of unsigned expression < 0 is always
false
example.c: In function 'main':
example.c:25: warning: comparison of unsigned expression < 0 is always
false
[root@doppelganger root]#

请注意，-Wall标志并不像大多数开发人员所期望的那样警告这种类型的错误。 为了生成这种类型bug的警告，必须使用-w标志。如果代码if(n<0)变为if(n<=0)，那么警告就不会发生因为这个条件已经不再成为可能。现在来看看真实世界的错误。下面的代码来自读入POST数据的PHP Apache模块(4.3.4)。(PHP 是这个世界上最好的语言（滑稽） —by译者)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/* {{{ sapi_apache_read_post
*/
static int sapi_apache_read_post(char *buffer,
							uint count_bytes TSRMLS_DC)
{
    uint total_read_bytes=0, read_bytes;
    request_rec *r = (request_rec *) SG(server_context);
    void (*handler)(int);
    /*
    * This handles the situation where the browser sends a
    * Expect: 100-continue header and needs to receive
    * confirmation from the server on whether or not it
    * can send the rest of the request. RFC 2616
    *
    */
    if (!SG(read_post_bytes) && !ap_should_client_block(r)) {
	    return total_read_bytes;
    }
    handler = signal(SIGPIPE, SIG_IGN);
    while (total_read_bytes<count_bytes) {
        /* start timeout timer */
        hard_timeout("Read POST information", r);
        read_bytes = get_client_block(r,
        buffer + total_read_bytes,
        count_bytes - total_read_bytes);
        reset_timeout(r);
        if (read_bytes<=) {
            break;
        }
        total_read_bytes += read_bytes;
    }
    signal(SIGPIPE, handler);
    return total_read_bytes;
}

从get_client_block()返回的值会被存在read_bytes变量中然后做比较来确定没有返回负值。因为raed_bytes是无符号的，这个检查就不会从get_client_block()中得到任何错误。不过事实证明，这个bug并不能在这个函数中立刻实施漏洞利用，你能看出来为什么吗？循环的控制中也有一个无符号比较，因此如果total_read_bytes减到0以下就会产生下溢，因此，得到一个比count_bytes还要大的值，然后循环结束。

审计技巧

检查比较对于审计C代码是必不可少的。特别注意保护分配(protect allocation)、数组索引和复制操作的比较。检验这些比较的最好方法是逐行仔细研究每个相关的表达式。

通常，你应该跟踪每个变量及其底层数据类型。如果可以将函数的输入追溯到熟悉的源，那么应该对每个输入变量可能具有的值有一个很好的了解。继续进行每个可能有趣的计算或比较，并在函数求值的不同点跟踪变量的可能值。你可以使用类似于前一节中查找整数边界条件问题所概述的过程。

在计算比较时，一定要注意有无符号整数值，以免它们的对等操作数被提升为无符号整型。sizeof和strlen()是导致这种提升的操作数的经典例子。

记住一定要注意无符号变量在比较中的使用，就像下面的这样：

1
2
if (uvar < 0) ...
if (uvar <= 0) ...

第一种形式会让编译器抛出警告，但第二种不会。如果你看到了这样的代码，那么一定会在这一节中的代码找到一些错误。 你应该仔细地逐行分析周围代码的功能。

7.2.7 运算符

运算符可以产生意想不到的结果。如你所见，在简单算术操作中使用未净化的(unsantilized)操作数可能会在应用程序中打开安全漏洞。这些漏洞曝光通常是跨越影响结果意义的边界条件的结果。此外，每个操作符都有关联的类型提升，这些提升隐式地对每个操作数执行，可能会产生一些意外的结果。由于产生意外结果是漏洞发现的本质，所以了解如何产生这些结果以及可能出现什么异常情况是很重要的。下面几节将重点介绍这些异常情况，并解释可能导致潜在漏洞的一些常见操作符误用。

sizeof运算符

第一个值得提及的运算符是sizeof。它经常被用在缓冲区分配，大小比较，以及和长度有关函数的长度变量中。sizeof运算符在某些情况下很容易被误用，这可能会在看起来很坚固的代码中导致一些微妙的漏洞。

sizeof最常见的错误之一就是在指针上不小心的误用。下面的代码展示了这样的类型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
char *read_username(int sockfd)
{
    char *buffer, *style, userstring[1024];
    int i;
    buffer = (char *)malloc(1024);
    if(!buffer){
        error("buffer allocation failed: %m");
        return NULL;
    }
    if(read(sockfd, userstring, sizeof(userstring)-1) <= 0){
        free(buffer);
        error("read failure: %m");
        return NULL;
    }
    userstring[sizeof(userstring)-1] = '\0';
    style = strchr(userstring, ':');
    if(style)
    	*style++ = '\0';
    sprintf(buffer, "username=%.32s", userstring);
    if(style)
    	snprintf(buffer, sizeof(buffer)-strlen(buffer)-1,
    ", style=%s\n", style);
    return buffer;
}

在这份代码中，一些用户数据从网络中读入然后被复制到分配后的缓冲区中。然而，sizeof在buffer中误用了。直觉上sizeof(buffer)会返回1024，但是由于它用在了符号指针类型上，因此它只会返回4！这个结果会在style值存在时导致snprintf()的长度参数整数下溢；最后的后果就是任意数量的数据会被写入buffer变量指向的地址位置。这个错误非常容易犯，并且经常在读代码时不被注意到，因此要格外小心被传入sizeof运算符变量的类型。 它们最经常出现在长度参数中，如前面的示例中所示，但是在为分配空间而计算长度时，偶尔也会出现。这种类型的错误很少出现的原因是，错误的分配可能会导致程序崩溃，因此，在许多应用程序的发布之前就会被捕获(除非是在很少被遍历的代码路径中)。

sizeof()也会在带符号和无符号变量的比较漏洞(在前面的小节“比较”中)，同时也在结构体填充问题(structure padding issues)(在本章后面“结构体填充”小节介绍)担任重要角色。

审计技巧：sizeof

要注意使用sizeof的情况，即开发人员在打算获取缓冲区的大小时获取指向缓冲区的指针的大小。这通常是由于编辑错误造成的，即缓冲区从函数内部移动到传递到函数中。

同样，在表达式中查找导致操作数转换为无符号值的sizeof。

出人意料的结果

你已经探索了算术运算符的两个主要特性:与整数类型存储相关的边界条件，以及在表达式中使用算术运算符时发生的转换所引起的问题。C的其他一些细微差别可能导致未预料到的行为，特别是与底层机器代码(underlying machine primitives)意识到符号相关的细微差别。如果预期结果在特定范围内，攻击者有时会违背这些预期。

有趣的是，在二进制补码机器中，在C中只有少数运算符的符号性(sign-ness)可以影响操作的结果。这些运算符中最重要的运算符是比较。除了比较之外，只有其他三个C操作符的结果对操作数是否有符号敏感:右移(>>)、除法(/)和取模(%)。当这些操作符与带符号操作数一起使用时，可能会产生意外的负结果，因为它们的底层机器级操作是可以识别符号的。作为代码审查人员，你应该注意这些操作符的滥用，因为它们可能产生超出预期值范围的结果，并使开发人员措手不及。

右移运算符(>>)常用于应用程序中代替除法运算符(在除以2的乘方时)。当使用带符号整数作为左操作数时，可能会出现问题。当右移一个负值时，执行符号位扩展算术移位(arithmetic shift)的底层机器保留该值的符号。这种保留符号的右移如下面代码所示：

1
2
3
4
signed char c = 0x80;
c >>= 4;
1000 0000 value before right shift
1111 1000 value after right shift

下面的代码显示了上面这段代码如何产生导致漏洞的意外结果。它接近于最近在客户端代码中发现的一个实际漏洞。

1
2
3
4
5
6
int print_high_word(int number)
{
    char buf[sizeof("65535")];
    sprintf(buf, "%u", number >> 16);
    return 0;
}

这个函数是设计用来打印一个16位的带符号整数(number变量的高16位)。由于number是带符号的，因此number如果是负数就会发生符号位扩展右移。 所以，sprintf()的%u说明符可以打印比为目标缓冲区分配的空间大小sizeof("65535")大得多的数字，结果就是缓冲区溢出。

易受攻击的右移是一些bug的好例子，这些bug在源代码中很难定位，但在汇编代码中却很容易看到。在Intel汇编代码中，sar助记符执行一种有符号的或算术的右移。shr助记符执行逻辑或无符号右移。因此，分析汇编代码可以帮助你确定右移是否可能容易受到签名扩展的影响。下表显示了汇编代码中的有符号和无符号右移操作。

带符号右移运算符 无符号右移运算符
mov eax, [ebp+8] mov eax, [ebp+8]
sar eax, 16 shr eax, 16
push eax push eax
push offset string push offset string
lea eax, [ebp+var_8] lea eax, [ebp+var_8]
push eax push eax
call sprintf call sprintf

除法(/)是另一个可以造成出人意料结果的运算符，同样是出于符号的原因。只要有一边操作数是负值， 得到的商也是负的。通常，在对整数进行除法时，应用程序通常不会考虑负结果的可能性。下面的代码展示了在除法中使用负值操作数的漏洞：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int read_data(int sockfd)
{
    int bitlength;
    char *buffer;
    bitlength = network_get_int(length);
    buffer = (char *)malloc(bitlength / 8 + 1);
    if (buffer == NULL)
    	die("no memory");
    if(read(sockfd, buffer, bitlength / 8) < 0){
        error("read error: %m");
        return -1;
    }
    return 0;
}

这份代码中从网络中取出bitlength参数然后基于次分配内存。bitlength除以8以得到接下来从套接字中读取的数据需要的字节数。并且结果加了1，用来储存除以8余下的那一部分位数。如果除法能够用来返回-1，那么加上1之后就是0，最后导致malloc返回一个分配了的非常小的内存。然后read()的第三个变量将会是-1，然后被转换为size_t后解释为一个非常大的正数值。

相似地，取模运算符(%)也会在应对负操作数时产生负值。代码审计人员应该注意没有正确地清理(santilize)操作数的取模操作，因为它们可能产生负面结果，从而导致安全性暴露。模运算符通常用于处理固定大小的数组(比如哈希表)，因此负的结果可以立即在数组开始前面索引，如下面代码所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#define SESSION_SIZE 1024
struct session {
    struct session *next;
    int session_id;
}
struct header {
    int session_id;
    ...
};
struct session *sessions[SESSION_SIZE];
struct session *session_new(int session_id)
{
    struct session *new1, *tmp;
    new1 = malloc(sizeof(struct session));
    if(!new1)
    die("malloc: %m");
    new1->session_id = session_id;
    new1->next = NULL;
    if(!sessions[session_id%(SESSION_SIZE-1)])
    {
        sessions[session_id%(SESSION_SIZE-1] = new1;
        return new1;
    }
	for(tmp = sessions[session_id%(SESSION_SIZE-1)]; 				tmp->next; tmp = tmp->next);
	tmp->next = new1;
	return new1;
}
int read_packet(int sockfd)
{
    struct session *session;
    struct header hdr;
    if(full_read(sockfd, (void *)&hdr, sizeof(hdr)) !=
    sizeof(hdr))
    {
        error("read: %m");
        return 1;
    }
    if((session = session_find(hdr.session_id)) == NULL)
    {
        session = session_new(hdr.sessionid);
        return 0;
    }
	... validate packet with session ...
	return 0;
}

正如你所见，首先从网络中读取头， 会话(session)的信息根据头的会话标识符字段(identifier field)从哈希表检索。 所有会话会存储在sessions哈希表中以便稍后由程序检索。如果session标识符是负数，那么取模运算的值也是负数，然后sessions的越界元素会被检索，也可能会被写入，然后造成可以利用的条件。

与右移操作符一样，无符号和有符号的除法和模数操作在Intel汇编代码中可以很容易地加以区分。无符号除法指令的助记符是div，有符号的对应指令是idiv。下表显示了有符号除法和无符号除法操作之间的区别。注意，当除数为常数时，编译器通常使用右移操作而不是除法。

带符号除法操作 无符号除法操作
mov eax, [ebp+8] mov eax, [ebp+8]
mov ecx, [ebp+c] mov ecx, [ebp+c]
cdq cdq
idiv ecx div ecx
ret ret

审计技巧：出人意料的结果

每当遇到右移位时，一定要检查左操作数是否有符号。如果是这样，则可能存在轻微的潜在漏洞。类似地，寻找具有符号操作数的取模和除法操作。如果用户可以指定负值，则可能会导致意外的结果。

译者注

在“出人意料的结果”这一小节，作者只是在编译的角度去解释对一些语法的误用导致的意外结果。但在链接过程中也会产生意外结果，本质上是全局变量区域(ELF中是.data,.bss节)符号的重复定义导致的，比如下面的这种例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// main.c
#include <stdio.h>
int d = 100;
int x = 200;
void p1(void);
int main(){
        p1();
        printf("d=%d,x=%d\n",d,x);
        return 0;
}
// p1.c
double d;

void p1(){
        d = 1.0;
}

//output: d=0,x=1072693248 (Ubuntu 16.04，gcc 5.4.0)

在这里，p1.c中的d是弱符号(即给出声明，没有定义值)，main.c里的d是强符号(即定义了值)，按照链接规则，多次定义的符号取强符号为准，然后在汇编级别就导致了一个double的赋值绕过了编译阶段的常规算术转换直接在位模式上赋到了int里，向main.c中的d和x位置上写入了8个字节。

不过这种级别的错误编译器会抛出警告，加了extern甚至编译器就不抛出警告了。

7.2.8 指针运算

指针通常是初学C编程的人遇到的第一个主要障碍，因为它们很难理解。涉及指针运算、解引用和间接指向(indirection, i.e. 指针指向指针 —by译者)、按值传递语义、指针操作符优先级和数组的伪等价(pseudo-equivalence)的规则可能很难学习。下面几节将重点讨论指针运算的几个方面，这些方面可能会让开发人员措手不及，并导致可能的安全暴露。

指针概述

你知道一个指针本质上是一个在内存地址的位置，所以它是一个数据类型，并且必须是实现依赖的。在不同的体系结构上，指针的表示可能会有显著的不同，即使在32位的Intel体系结构上，指针也可以以不同的方式实现。例如，你可以使用基于16位的代码，甚至可以使用透明地支持包含段的自定义虚拟内存方案的编译器。因此，以下讨论假设使用GCC或vc++编译器的通用架构来编写英特尔机器上的用户代码。

你知道，指针可能必须是无符号整数，因为有效虚拟内存地址的范围从0x0到0xffffffff。也就是说，当你减去两个指针时，它看起来有点奇怪。难道指针不需要以某种方式表示负值吗?所以减法的结果根本不是一个指针;相反，它是一个有符号整数类型，称为ptrdiff_t。

通过强制类型转换，指针可以自由地转换为整数和其他类型的指针。但是，编译器不保证结果指针或整数正确对齐或指向有效对象。因此，指针是C语言中更依赖于实现的部分之一。

指针运算概述

当你你在做指针运算时会发生什么？下面时一个简单的给指针加1的例子：

1
2
short *j;j=(short *)0x1234;
j = j + 1;

这份代码中有一个名为j的指针。它初始化为任意的不变地址，0x1234.这是一份很差劲的C代码，但也值得用来讨论我们指向的内容。就像前面所提到的，你可以将指针在强制类型转换后当作整数使用，但结果取决于实现。你可能假设当你将j加1后会得到0x1235。然而，这不会发生，j的值应该时0x1236才对。

当C执行涉及指针的算术运算时，它会相对于指针目标的大小执行操作。所以当你给一个对象的指针加1时，结果是一个指向内存中下一个相同大小的对象的指针。在本例中，对象是一个short整数，占用2个字节(在32位Intel架构中)，因此内存中紧跟在0x1234后面的short整数位于0x1236位置。如果减去1，结果是在0x1234之前的short的地址，即0x1232。如果加5，就会得到地址0x123e，它是距离0x1234的第5个short的地址。

另一种考虑方法是，将一个指向对象的指针视为由该对象的一个元素组成的数组。所以j，一个指向short的指针，被当作数组short j[1]，它包含一个short。因此，j + 2就等于&j[2]。下表显示了这个概念。

指针表达式 数组表达式 地址
j-2 &j[-2] 0x1230
j-1 &j[-1] 0x1232
j j 或者 &j[0] 0x1234
j+1 &j[1] 0x1236
j+2 &j[2] 0x1238
j+3 &j[3] 0x123a
j+4 &j[4] 0x123c
j+5 &j[5] 0x123e

现在看看重要的指针算术运算符的详细信息，这将在以下部分中介绍。

加法

指针加法的规则比你预期的要严格一些。可以将整数类型添加到指针类型或将指针类型添加到整数类型，但不能将指针类型添加到指针类型。考虑指针加法实际上是做什么是有意义的;编译器不会知道哪个指针用作基类型，哪个指针用作索引。例如，看看下面的操作：

1
2
3
unsigned short *j;
unsigned long *k;
x = j+k;

这个操作是无效的，因为编译器不知道如何将j或k转换为指针运算的索引。你当然可以将j或k转换为整数，但结果可能出乎意料，而且不太可能有人有意这样做 。

C语言的一个有趣规则是下标操作符属于指针加法的范畴。C标准声明下标运算符等价于以下方式涉及加法的表达式：

1
E1[E2] 等价于 (*((E1)+(E2)))

记住这一点，看看下面的例子 ：

1
char b[10];b[4]='a';

表达式b[4]表示符号数组b的第5个元素。根据上面的规则，对于这个写入操作有以下等价的方法：

1
(*((b)+(4)))='a';

从前面的分析中你已经知道了b+4代表什么，由于b是指向char的指针，因此它就等于在说&b[4]；因此，这个表达式也就是在说(*(&b[4]))或者b[4]。

最后，请注意整数和指针之间的加法的结果类型就是指针的类型。

减法

减法的规则与加法相似，但只允许从一个指针减去另一个指针。当你从相同类型的指针中减去一个指针时，你要求的是两个元素下标的差。因此，减法结果类型不是指针，而是ptrdiff_t，它是有符号整数类型。C标准指出应该在stddef.h头文件中定义它。

比较

指针之间的比较就像你所期望的那样。他们考虑两个指针在虚拟地址空间中的相对位置。结果类型与其他比较相同:包含1或0的整数类型

条件运算符

条件运算符(?)可以使用指针作为它的最后两个操作数，并且必须协调它们的类型，就像使用算术操作数一样。它通过将指针类型的所有限定符应用到结果类型来实现这一点。

漏洞

涉及指针运算的漏洞很少被广泛报道，至少在写这本书时是这样的。许多涉及字符指针操作的漏洞本质上都归结为对缓冲区大小的错误计算，尽管它们在技术上被定义为指针运算错误，但它们并不像指针漏洞那样微妙。更有害的问题形式是，开发人员错误地对指针执行算术运算，而没有意识到它们的整数操作数是按指针目标的大小缩放的。考虑以下代码：

1
2
3
4
5
6
int buf[1024];
int *b=buf;
while (havedata() && b < buf + sizeof(buf))
{
	*b++=parseint(getdata());
}

b < buf + sizeof(buf)是为了阻止b向前推进时超过buf[1023]。然而，它实际上却阻止b超过buf[4092]。因此，这段代码可能容易出现相当简单的缓冲区溢出。

下面的代码分配了一个缓冲区然后将参数字符串中的第一个路径组件复制到缓冲区中。 一个长度检查用来保护wscat函数不会溢出分配的缓冲区，然而它的构造不正确。因为字符串是宽字符类型，指针减法(sep-string)检查输入大小返回两个指针的宽字符之差。也就是两个指针数值之差除以2.因此，只要sep-string小于(MAXCHARS*2)那么检查就会成功，这是分配的缓冲区两倍空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
wchar_t *copy_data(wchar_t *string)
{
    wchar *sep, *new;
    int size = MAXCHARS * sizeof(wchar);
    new = (wchar *)xmalloc(size);
    *new = '\0';
    if(*string != '/'){
        wcscpy(new, "/");
        size -= sizeof(wchar_t);
    }
    sep = wstrchr(string, '/');
    if(!sep)
    	sep = string + wcslen(string);
    if(sep - string >= (size-sizeof(wchar_t))
    {
        free(new);
        die("too much data");
    }
    *sep = '\0';
    wcscat(new, string);
    return new;
}
审计技巧

指针运算错误可能很难发现。每当执行涉及指针的算术运算时，查找那些指针的类型，然后检查操作是否与所发生的隐式运算一致。在上面的代码中，sizeof()是否被错误地用于指向非单字节类型的指针?是否发生过类似的操作，开发人员假设指针类型不会影响操作的执行?

7.2.9 其他C的细微差别

下面几节将讨论C语言的特性和可能会出现与安全性相关错误的黑暗角落。这些漏洞的实际例子并不多，但是你仍然应该意识到潜在的风险。有些示例可能看起来是人为设计的，但是尝试将它们想象为隐藏在宏层和相互依赖的函数之下，这样看起来可能更现实。

运算顺序

对于大多数操作符，C不能保证操作数求值的顺序或表达式“副作用”赋值的顺序。例如，考虑以下代码：

1
printf("%d\n", i++, i++);

我们不能保证这两个增量的执行顺序，你会发现输出会根据编译器和编译程序的体系结构而变化。保证计算顺序的唯一运算符是&&，||，?:，和,。注意逗号不是指函数的参数;它们的运算顺序是由实现定义的。因此，在如下简单代码中，不能保证在b()之前调用a():

1
x = a() + b();

模棱两可的副作用与模棱两可的运算顺序略有不同，但是它们有相似的结果。副作用是导致修改变量赋值或增量运算符(如++)的表达式。副作用的求值顺序没有在同一个表达式中定义，因此如下内容是已定义的实现，并可能会导致问题：

1
a[i] = i++;

这些问题会导致什么样的安全后果？在下面的代码中， 开发人员使用getstr()调用来获取用户字符串并从外部源传递字符串。但是，如果重新编译了系统，并且getstr()函数的运算顺序发生了变化，那么代码最终可能会记录密码而不是用户名。诚然，这是一个在测试过程中就能发现的低风险问题。

1
2
3
4
5
6
7
8
9
10
11
12
int check_password(char *user, char *pass)
{
    if (strcmp(getpass(user), pass))
    {
        logprintf("bad password for user %s\n", user);
        return -1;
    }
    return 0;
}
...
if (check_password(getstr(), getstr())
	exit(1);

下面的代码有一个copy_packet()函数用来从网络中读取包。它使用GET32()宏将一个整数送入包中然后将指针向前移动。协议中有一个可选填充的规定，填充大小字段的存在是由数据包部头中的一个标志指示的。因此，如果设置了FLAG_PADDING，那么用于计算数据的GET32()宏的求值顺序可能会颠倒。如果填充选项是协议中相当未使用的部分，那么这种性质的错误在生产使用中可能不会被检测到。

1
2
3
4
5
6
7
8
9
10
11
12
13
#define GET32(x) (*((unsigned int *)(x))++)
u_char *copy_packet(u_char *packet)
{
    int *w = (int *)packet;
    unsigned int hdrvar, datasize;
    /* packet format is hdr var, data size, padding size */
    hdrvar = GET32(w);
    if (hdrvar & FLAG_PADDING)
    	datasize = GET32(w) - GET32(w);
    else
    	datasize = GET32(w);
    ...
}

结构体填充

C结构体的一个有点模糊的特性是，结构成员不必在内存中连续地布局。成员的顺序保证遵循程序员指定的顺序，但是可以在成员之间使用结构填充来促进对齐和性能需求。这里有一个简单结构体的例子：

1
2
3
4
5
6
struct bob
{
    int a;
    unsigned short b;
    unsigned char c;
};

你觉得sizeof(bob)会是什么？从道理上说应该是7，也就是sizeof(a)+sizeof(b)+sizeof(c)，也就是4+2+1。但大多数编译器会返回8因为它们插入了结构体填充。 这种行为现在还不太清楚，但是随着更多64位代码的引入，它肯定会成为一个众所周知的现象，因为它可能会对这段代码产生更严重的影响。 这会造成怎样的安全问题？考虑下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
struct netdata
{
    unsigned int query_id;
    unsigned short header_flags;
    unsigned int sequence_number;
};
int packet_check_replay(unsigned char *buf, size_t len)
{
    struct netdata *n = (struct netdata *)buf;
    if ((ntohl(n->sequence_number) <= g_last_sequence number)
    return PARSE_REPLAYATTACK;
    // packet is safe - process
    return PARSE_SAFE;
}

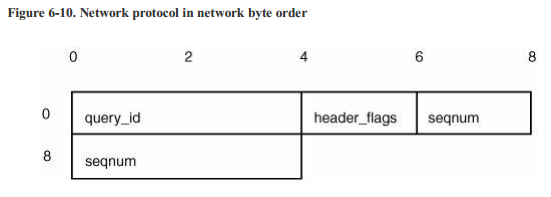
在32位大端系统中，netdata结构体会像图6-9那样布局。一个unsigned int，一个unsigned short，两个字节的填充，一个unsigned int，因此结构体总的大小是12字节。图6-10显示了在网络中的布局。如果开发者没有预料到结构体填充的插入，那么他们就可能会将网络协议的解释写错。 此错误可能导致服务器接受重放攻击(replay attack)。

figure 6-9:

6-9
6-10

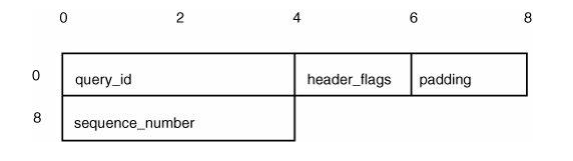
在64位体系架构中，犯这种错误的可能性会增加。如果一个结构包含一个指针或long值，结构在内存中的布局很可能会改变。任何64位的值，例如指针或长整型，都将占用32位系统的两倍空间，并且必须放置在64位对齐边界上。

填充位的内容取决于分配结构时内存中的内容。这些位可能不同，这可能导致涉及内存比较的逻辑错误，如下面代码所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
struct sh
{
    void *base;
    unsigned char code;
    void *descptr;
};
void free_sechdrs(struct sh *a, struct sh *b)
{
    if (!memcmp(a, b, sizeof(a)))
    {
        /* they are equivalent */
        free(a->descptr);
        free(a->base);
        free(a);
        return;
    }
    free(a->descptr);
    free(a->base);
    free(a);
    free(b->descptr);
    free(b->base);
    free(b);
    return;
}

如果两个结构体的填充是不同的，那么久可能造成双重释放错误(double-free error)的发生。看看下面的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
struct hdr
{
    int flags;
    short len;
};
struct hdropt
{
    char opt1;
    char optlen;
    char descl;
};
struct msghdr
{
    struct hdr h;
    struct hdropt o;
};
struct msghdr *form_hdr(struct hdr *h, struct hdropt *o)
{
    struct msghdr *m=xmalloc(sizeof *h + sizeof *o);
    memset(m, 0, sizeof(struct msghdr));
	..

hdropt的大小应该是3，因为出于对齐原因不会有填充。hdr的大小应该是8，由于对其的要求msghdr的大小应该是12。因此，menset就会超过分配的数据写入1个字节的\0。

优先级

当你查看由有经验的开发人员编写的代码时，你经常会看到复杂的表达式似乎没有括号。一个有趣的漏洞可能是这样一种情况:犯了优先级错误，但发生的方式不会完全中断程序。

第一个潜在问题是位级别操作符&和|的优先级，特别是当你将它们与比较和相等操作符混合使用时，如本例所示：

1
2
3
4
if ( len & 0x80000000 != 0)
	die("bad len!");
if (len < 1024)
	memcpy(dst, src, len);

程序员试图通过检查最高位来判断它是否为负值。他的意图就像这样：

1
2
if ( (len & 0x80000000) != 0)
	die("bad len!");

然而代码实际做的是这样：

1
2
if ( len & (0x80000000 != 0))
	die("bad len!");

这份代码最终会评估len & 1。如果len的最小有效位没有设置。那么测试就会通过，用户将能够把一个负值传入mencpy()。

还有一些涉及赋值的潜在优先级问题，但是由于编译器的警告，这些问题不太可能出现在生产代码中。例如，看看下面的代码;

1
2
if (len = getlen() > 30)
    snprintf(dst, len - 30, "%s", src)

代码的作者想做这样的事情：

1
2
if ((len = getlen()) > 30)
    snprintf(dst, len - 30, "%s", src)

然而代码却会这样做：

1
2
if (len = (getlen() > 30))
    snprintf(dst, len - 30, "%s", src)

len会在if语句后变为1或者0.如果为1，那么第二个snprintf()的变量就会说-29，这实际上是一个无限的字符串。

下面是另一个更潜在的优先级错误：

1
int a = b + c >> 3;

代码的作者想做这样的事情：

1
int a = b + (c >> 3);

正如你所想，代码会实际这样做：

1
int a = (b + c) >> 3;

宏/预处理器

C的预处理器也可能成为安全问题的源头。许多人都熟悉像这样的宏：

1
#define SQUARE(x) x*x

如果像这样使用：

1
y = SQUARE(z + t);

那么就会做这样的事情：

1
y = z + t*z + t;

结果显然是错误的。推荐的修复的方法是在宏里加上括号，就像下面这样：

1
#define SQUARE(x) ((x)*(x))

在考虑求值顺序和副作用问题时，用这种方式构造的宏仍然会遇到麻烦。例如，如果你使用以下方法：

1
y = SQUARE(j++);

宏会展开为：

1
y = ((j++)*(j++));

于是结果就成为了实现定义的了。相似地，如果你这样做：

1
y = SQUARE(getint());

宏会展开为：

1
y = ((getint())*(getint()));

这个结果可能不是作者想要的。如果宏在主流使用方法之外使用，则肯定会引入安全问题，因此在审计大量使用宏的代码时要多加注意。如果有疑问，可以手动展开它们，或者查看预处理器通过的输出。

拼写错误

程序员可能会犯许多简单的拼写错误，这些错误可能不会影响程序编译或中断程序的运行时进程，但是这些拼写错误可能会导致与安全性相关的问题。这些错误在生产代码中很少出现，但偶尔也会出现。尝试发现代码中的拼写错误可能很有趣。可能出现的拼写错误已经作为一系列的挑战提出。在阅读分析之前，试着找出错误。

1
2
3
4
5
6
7
8
// 挑战1
while (*src && left)
{
    *dst++=*src++;
    if (left = 0)
    die("badlen");
    left--;
}

if (left = 0)应该写成if (left == 0)才对。

在正确的代码版本中，如果left为0，则循环检测缓冲区溢出尝试并终止。在不正确的版本中，if语句将0赋值给left，赋值的结果是0。if(0)不为真，那么接下来发生的是left--。因为left是0,left--就变成了- 1或者一个大的正数，这取决于left的类型。不管怎样，left都不是0，因此while循环继续进行，并且检查不能防止缓冲区溢出。

1
2
3
4
5
6
7
8
//挑战2
int f;
f=get_security_flags(username);
if (f = FLAG_AUTHENTICATED)
{
	return LOGIN_OK;
}
return LOGIN_FAILED;

语句if (f = FLAG_AUTHENTICATED)应该这样写：

1
if (f == FLAG_AUTHENTICATED)

在代码的正确版本中，如果用户的安全标志表明他们已经过身份验证，则函数返回LOGIN_OK。否则，返回LOGIN_FAILED。在不正确的版本中，if语句将FLAG_AUTHENTICATED赋值给f。if语句总是成功，因为FLAG_AUTHENTICATED是某个非零值。因此，该函数为每个用户返回LOGIN_OK。

1
2
3
4
5
// 挑战3
for (i==5; src[i] && i<10; i++)
{
	dst[i-5]=src[i];
}

语句for (i==5; src[i] && i<10; i++)应该这样写：

1
for (i=5; src[i] && i<10; i++)

在代码的正确版本中，for循环复制4个字节，从src[5]开始读取并开始写入dst[0]。在错误的版本中，表达式i=的值为真或假，但并不影响i的内容。因此，如果i小于10，它可能会导致for循环在dst和src缓冲区的边界之外读写。

1
2
3
4
// 挑战4
if (get_string(src) &&
	check_for_overflow(src) & copy_string(dst,src))
	printf("string safely copied\n");

if声明应该像这样：

1
if (get_string(src) &&	check_for_overflow(src) && copy_string(dst,src))

在代码的正确版本中，程序将一个字符串放入src缓冲区并检查src缓冲区是否有溢出。如果没有溢出，它将字符串复制到dst缓冲区并打印“string safely copied”。

在错误版本中，&运算符与&&运算符没有相同的特征。在这种情况下，即使不存在逻辑与位操作的差异造成的问题，也存在短路评估(short-circuit evaluation)和按顺序执行(graranteed order of execution)的关键问题。因为它是按位AND运算，所以两个操作数表达式都要求值，而它们求值的顺序不一定是已知的。因此，即使check_for_overflow()失败，也会调用copy_string()，并且可能会在调用check_for_overflow()之前调用它。

1
2
3
// 挑战5
if (len > 0 && len <= sizeof(dst));
	memcpy(dst, src, len);

if声明应该像这样：

1
if (len > 0 && len <= sizeof(dst))

在正确的代码版本中，程序仅在长度在一定范围内时执行memcpy()，从而防止缓冲区溢出攻击。在不正确的版本中，if语句末尾的额外分号表示一个空语句，这意味着memcpy()始终运行，而不管长度检查的结果如何。

1
2
3
// 挑战6
char buf[040];
snprintf(buf, 40, "%s", userinput);

语句char buf[040];应该写为char buf[40];。

在代码的正确版本中，程序为用于复制用户输入的缓冲区留出40个字节。在不正确的版本中，程序设置了32个字节。在C语言中，当整数常量前面有0时，它指示编译器该常量是八进制的。因此，缓冲区长度被解释为八进制040或十进制32，并且snprintf()可以写入超过堆栈缓冲区的末尾。

1
2
3
4
5
// 挑战7
if (len < 0 || len > sizeof(dst)) /* check the length
	die("bad length!");
/* length ok */
memcpy(dst, src, len);

if语句应该这样写：

1
if (len < 0 || len > sizeof(dst)) /* check the length */

在代码的正确版本中，程序在执行memcpy()之前检查长度，如果长度超出了适当的范围，则调用abort()。

在不正确的版本中，注释没有结束符号意味着memcpy()成为if语句的目标语句。所以memcpy()只在长度检查失败时发生。

1
2
3
4
5
6
// 挑战8
if (len > 0 && len <= sizeof(dst))
    copiedflag = 1;
    memcpy(dst, src, len);
if (!copiedflag)
    die("didn't copy");

第一个if语句应该这样写：

1
2
3
4
5
if (len > 0 && len <= sizeof(dst))
{
    copiedflag = 1;
    memcpy(dst, src, len);
}

在正确的版本中，程序在执行memcpy()之前检查长度。如果长度超出了适当的范围，程序将设置导致中止的标志。

在不正确的版本中，if语句后面缺少复合语句意味着始终执行memcpy()。缩进的目的是欺骗读者的眼睛。

1
2
3
4
5
6
7
// 挑战9
if (!strncmp(src, "magicword", 9))
	// report_magic(1);
if (len < 0 || len > sizeof(dst))
	assert("bad length!");
/* length ok */
memcpy(dst, src, len);

report_magic(1)语句应该这样写：

1
2
// report_magic(1);
;

在正确的版本中，程序在执行memcpy()之前检查长度。如果长度超出了适当的范围，程序将设置导致中止的标志。

在错误的版本中，在magicword if语句后面缺少复合语句意味着长度检查只在magicword比较为真时执行。因此，很可能总是执行memcpy()。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// 挑战10
l = msg_hdr.msg_len;
frag_off = msg_hdr.frag_off;
frag_len = msg_hdr.frag_len;
...
if ( frag_len > (unsigned long)max)
{
    al=SSL_AD_ILLEGAL_PARAMETER;
    SSLerr(SSL_F_DTLS1_GET_MESSAGE_FRAGMENT,
    SSL_R_EXCESSIVE_MESSAGE_SIZE);
    goto f_err;
}
if ( frag_len + s->init_num >
		(INT_MAX - DTLS1_HM_HEADER_LENGTH))
{
    al=SSL_AD_ILLEGAL_PARAMETER;
    SSLerr(SSL_F_DTLS1_GET_MESSAGE_FRAGMENT,
    SSL_R_EXCESSIVE_MESSAGE_SIZE);
    goto f_err;
}
if ( frag_len &
	!BUF_MEM_grow_clean(s->init_buf, (int)frag_len +
		DTLS1_HM_HEADER_LENGTH + s->init_num))
{
    SSLerr(SSL_F_DTLS1_GET_MESSAGE_FRAGMENT,
    ERR_R_BUF_LIB);
    goto err;
}
if ( s->d1->r_msg_hdr.frag_off == 0)
{
    s->s3->tmp.message_type = msg_hdr.type;
    s->d1->r_msg_hdr.type = msg_hdr.type;
    s->d1->r_msg_hdr.msg_len = l;
    /* s->d1->r_msg_hdr.seq = seq_num; */
}
/* XDTLS: ressurect this when restart is in place */
s->state=stn;
/* next state (stn) */
p = (unsigned char *)s->init_buf->data;
if ( frag_len > 0)
{
    i=s->method->ssl_read_bytes(s,SSL3_RT_HANDSHAKE,
    &p[s->init_num],
    frag_len,0);
    /* XDTLS: fix thismessage fragments cannot
    span multiple packets */
    if (i <= 0)
    {
        s->rwstate=SSL_READING;
        *ok = 0;
		return i;
	}
}
else
	i = 0;

找到bug了吗？

在一次长度检查中，开发人员使用了按位的AND运算符(&)，而不是逻辑的AND运算符(&&)。具体来说，声明应该是这样的:

1
2
3
if ( frag_len &&
	!BUF_MEM_grow_clean(s->init_buf, (int)frag_len +
		DTLS1_HM_HEADER_LENGTH + s->init_num))

如果BUF_MEM_grow_clean()函数失败，这个简单的错误可能会导致内存损坏。如果失败，该函数将返回0，逻辑not运算将其设置为1。然后，将使用frag_len执行按位的AND操作。因此，在失败的情况下，畸形语句实际上执行以下操作:

1
2
3
4
if(frag_len & 1)
{
	SSLerr(...);
}

7.2.10 总结

本章讨论了C编程语言的细微差别，这些差别可能导致微妙和复杂的漏洞。这种背景应该使你能够识别操作符处理、类型转换、算术操作和常见的C输入错误可能出现的问题。然而，这一主题的复杂性并不足以让人一蹴而就地完全理解。因此，在进行应用程序审计时，请参阅本材料。毕竟，即使是最好的代码审计员也很容易忽略可能导致严重漏洞的细微错误。

wechat
scan and following my wechat official account.